When a resistor of $5 Ω$ is connected across a cell, its terminal potential differnce is balanced by 140 cm of potentiometer wire and when a resistance of $8 Ω$ is connected across the cell, the terminal potential difference is balanced by 160 cm of the potentiometer wire. Find the internal resistance of the cell.

Video Solution

Text Solution

Verified by Experts

Here, $R_{1} = 5 Ω, l_{1} = 140 c m$ ,
$R_{2} = 8 Ω, l_{2} = 160 c m$
Let emf of the cell be balanced by length l of the potnetiometer wire. Then as per question,
In the first case,
$r = R_{1} (\frac{l_{1} - l_{1}}{l_{1}}) or \frac{r l_{1}}{R_{1}} = l - l_{1}$
In the second case,
$r = R_{2} (\frac{l_{1} - l_{2}}{l_{2}}) or \frac{r l_{2}}{R_{2}} = l - l_{2}$
Subtracting (ii) from (i), we get
$r [\frac{l_{1}}{R_{1}} - \frac{l_{2}}{R_{2}}] = (l - l_{1}) - (l - l_{2}) = l_{2} - l_{1}$
or $r = \frac{l_{2} - l_{1}}{\frac{l_{1}}{R_{1}} - \frac{l_{2}}{R_{2}}} = \frac{160 - 140}{\frac{140}{5} - \frac{160}{8}} = 2.5 Ω$

Updated on:21/07/2023

In the given figure, battery E is balanced on 55 cm length of potentiometer wire but when a resistance of $10 Ω$ is connected in parallel with the battery then it balances on 50 cm length of the potentiometer wire then internal resistance r of the battery is

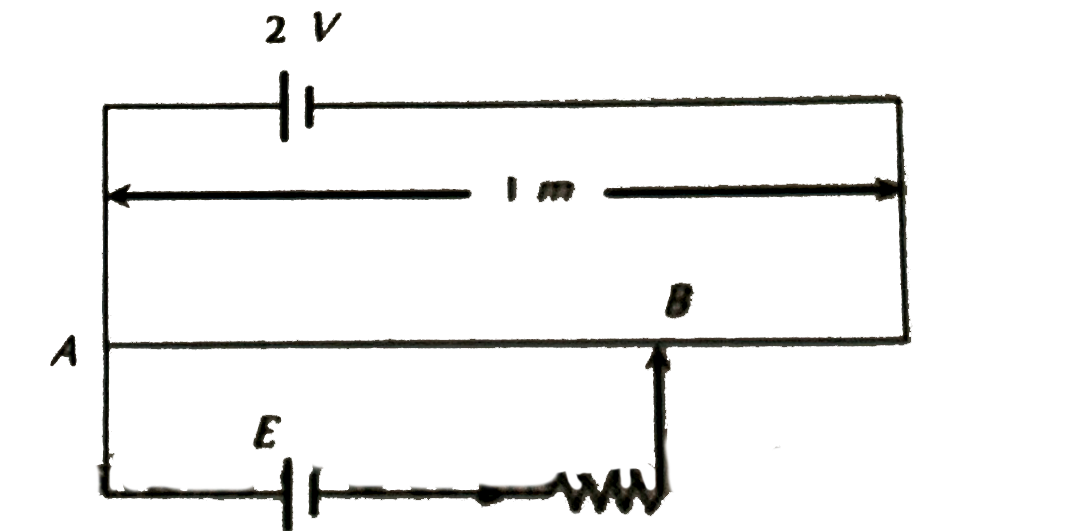A $1 Ω$
B $3 Ω$
C $10 Ω$
D $5 Ω$
In fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of $10 Ω$ is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-

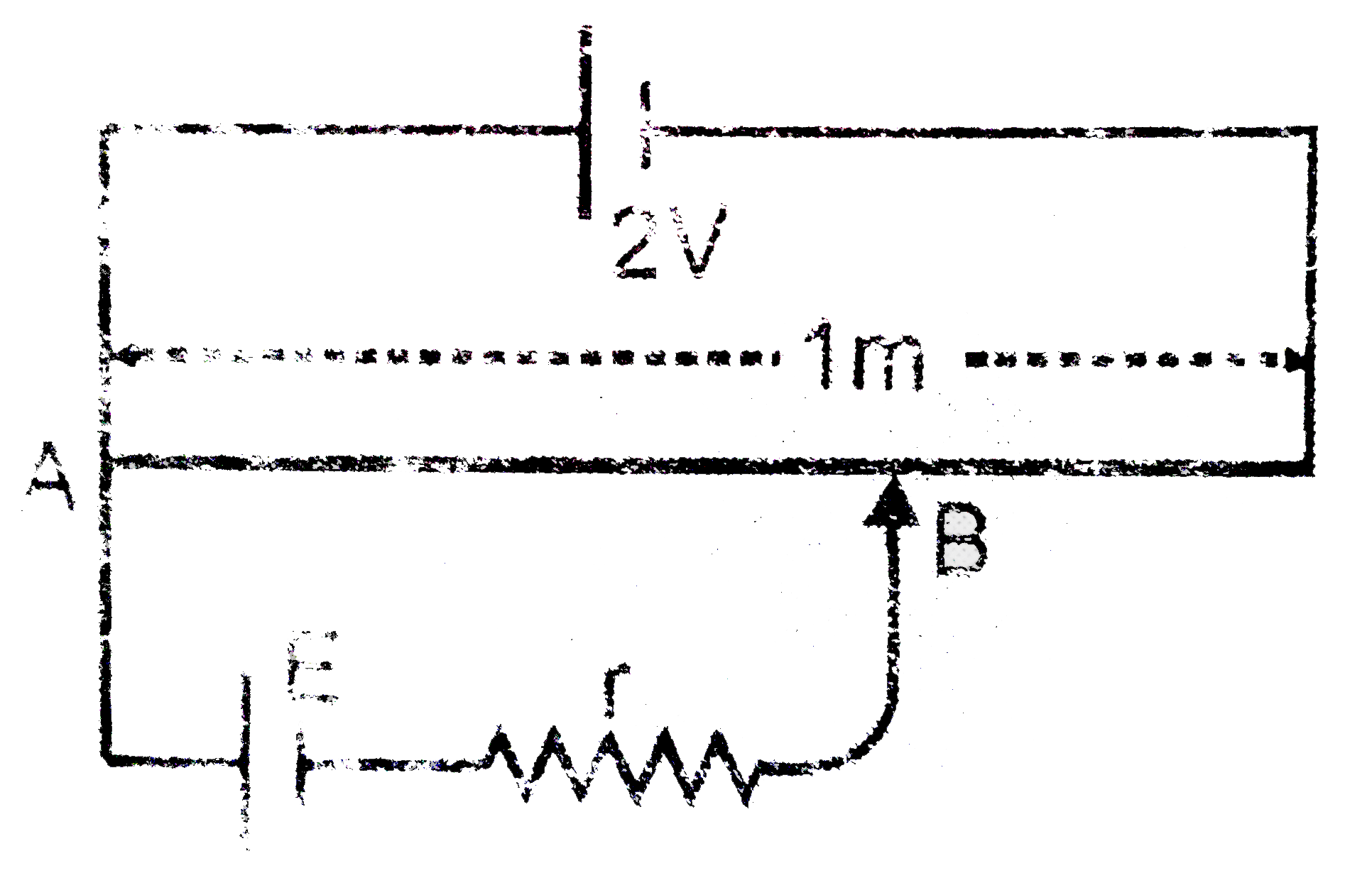A $1 Ω$
B $3 Ω$
C $10 Ω$
D $5 Ω$
The e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of $2 Ω$ is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
A $0.1 Ω$
B $1 Ω$
C $2 Ω$
D $0.5 Ω$