When a transparent parallel plate of uniform thickness t and refractive index μ is interposed normally in the path of a beam of light, the optical path is
(μ+1)t
(μ−1)t
(μ+1)t
μt
The correct Answer is:B
To solve the problem of finding the optical path when a transparent parallel plate of uniform thickness t and refractive index μ is interposed normally in the path of a beam of light, we can follow these steps:
1. Understanding Optical Path Length:
The optical path length (OPL) is defined as the product of the physical path length and the refractive index of the medium through which the light travels. When light passes through a medium with a refractive index μ, the optical path length can be expressed as:
OPL=Physical Path Length×μ
2. Identifying Physical Path Length:
In this case, the physical path length is simply the thickness of the parallel plate, which is t.
3. Calculating Optical Path Length:
Therefore, when light travels through the parallel plate, the optical path length becomes:
OPL=t×μ
4. Considering the Optical Path Change:
If there were no plate, the optical path length would just be the distance traveled in air (or vacuum), which we can consider as t (since the light travels through the same thickness in air). The optical path length in air is simply t.
5. Finding the Change in Optical Path:
The change in optical path length due to the introduction of the plate is given by:
ΔOPL=OPL with plate−OPL without plate
Substituting the values we have:
ΔOPL=(t⋅μ)−t
6. Factoring Out the Common Terms:
We can factor out t from the equation:
ΔOPL=t(μ−1)
7. Final Expression for Optical Path:
Thus, the optical path change when the transparent parallel plate is introduced is:
ΔOPL=t(μ−1)
Conclusion:
The optical path when a transparent parallel plate of uniform thickness t and refractive index μ is interposed normally in the path of a beam of light is given by:
ΔOPL=t(μ−1)
The optical path length (OPL) is defined as the product of the physical path length and the refractive index of the medium through which the light travels. When light passes through a medium with a refractive index μ, the optical path length can be expressed as:
OPL=Physical Path Length×μ
In this case, the physical path length is simply the thickness of the parallel plate, which is t.
Therefore, when light travels through the parallel plate, the optical path length becomes:
OPL=t×μ
If there were no plate, the optical path length would just be the distance traveled in air (or vacuum), which we can consider as t (since the light travels through the same thickness in air). The optical path length in air is simply t.
The change in optical path length due to the introduction of the plate is given by:
ΔOPL=OPL with plate−OPL without plate
Substituting the values we have:
ΔOPL=(t⋅μ)−t
We can factor out t from the equation:
ΔOPL=t(μ−1)
Thus, the optical path change when the transparent parallel plate is introduced is:
ΔOPL=t(μ−1)
The optical path when a transparent parallel plate of uniform thickness t and refractive index μ is interposed normally in the path of a beam of light is given by:
ΔOPL=t(μ−1)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - taking it together47videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion reason8videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions13videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER22videos
SOLVED PAPERS 2018
Similar Questions
A beam of light is converging towards a point. A plane parallel plate of glass of thickness t, refractive index μ is introduced in the path of the beam. The convergent point is shifted by (assume near normal incidence) :
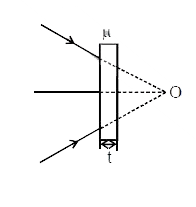 View Solution
View SolutionInterference pattern with Young's double slits 1.5mm apart are formed on a screen at a distance 1.5m from the plane of slits. In the path of the beam of one of the slits, a transparent film of 10 micron thickness and of refractive index 1.6 is interposed while in the path of the beam from the older slit a transparent film of 15 micron thickness and of refractive index 1.2 is interposed. Find the displacement of the fringe patten.
View SolutionA call is connected between the point A and C of a circular conductor ABCD of centre O with angle AOC=60∘ . If B1 and B2 are the magnitudes of the magnetic field at O due ti the currents In ADC respectively, the ratio B1B2 is
 View Solution
View SolutionLight travels through a glass plate of thickness t and refractive index μ. If c is the speed of light in vacuum, the time taken by light to travel this thickness of glass is
View SolutionA transparent slab of thickness t and refractive index μ is inserted in front of upper of YDSE apparauts. The wavelength of ligth used. is λ. Assume that there is no absorption of light by the slab. Mark the correct statement(s).
View SolutionThe figure shows a Young's double slit experimental setup. It is observed that when a thin transparent sheet of thickness t and refractive index μ is put front of one of the slits, the central maximum gets shifted by a distance equal to n fringe widths. If the wavelength of light used is λ, t will be :
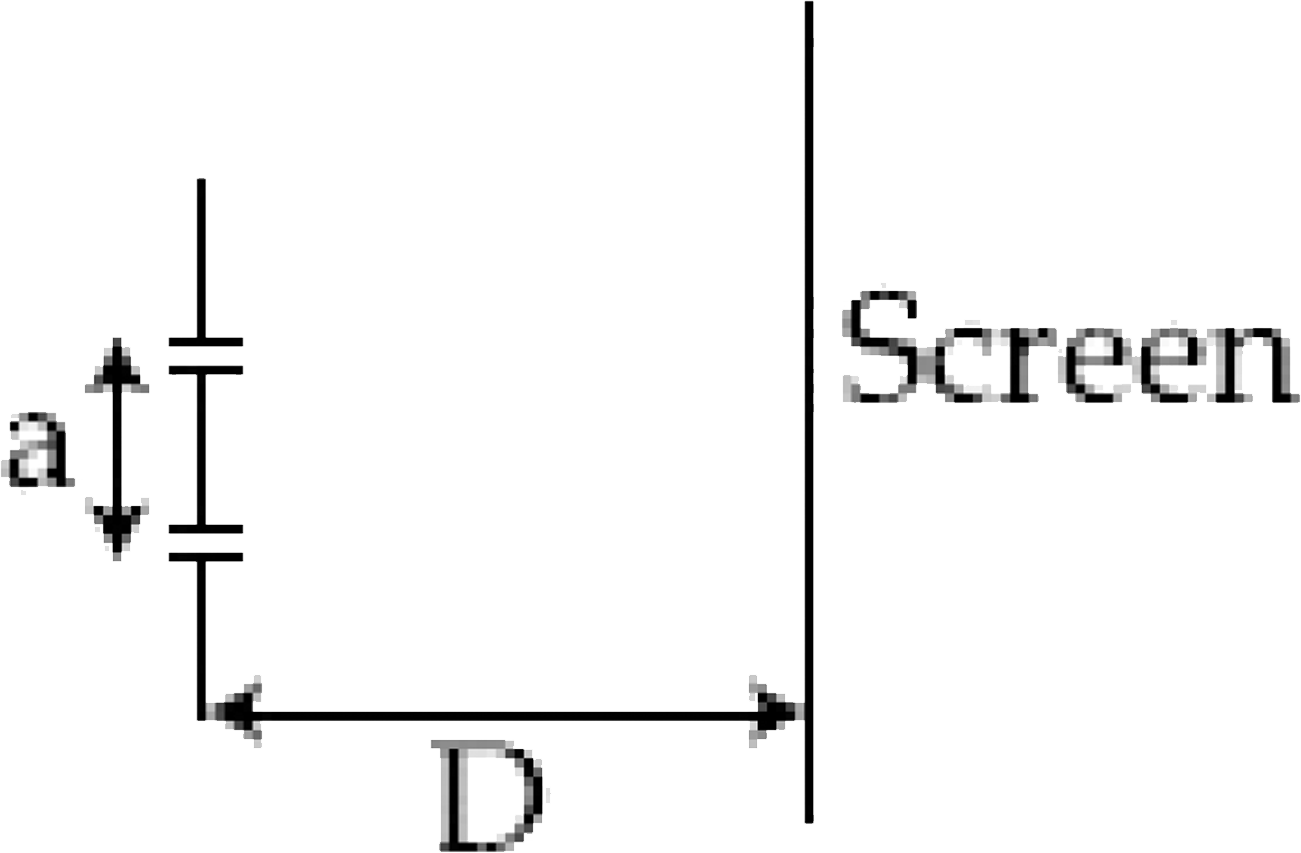 View Solution
View SolutionA double slit experiment is performed with light of wavelength 500nm. A thin film of thickness 2μm and refractive index 1.5 is introduced in the path of the upper beam. The location of the central maximum will
View SolutionA thin transparent film of thickness 3000 Å and refractive index 1.5 ud deposited on a sheet made of a metal. Assuming normal incidence of light and also that the film is a plane parallel one, what will be the color of a pot made from this sheet when observed in white light?
View SolutionA transparent glass plate of thickness 0.5 mm and refractive index 1.5 is placed infront of one of the slits in a double slit experiment. If the wavelength of light used is 6000A∘, the ratio of maximum to minimum intensity in the interference pattern is 25/4. Then the ratio of light intensity transmitted to incident on thin transparent glass plate is
View SolutionA beam of light is converging towards a point I on a screen. A plane glass plate whose thickness in the direction of the beam =t , refractive index =μ , is introduced in the path of the beam. The convergence point is shifted by
A. t(1−1μ) away
B. t(1+1μ) away
C. t(1−1μ) nearer
D. t(1+1μ) nearerView Solution

