When light of frequency v1 incident on a metal with work function W0 (where hv1>W0), the photocurrent falls to zero at a stopping potential of V1. If the frequency of light is increased to v2, the stopping potential changes to V2. Therefore, the charge of an electron is given by
W(υ2+υ1)υ1V2+υ1V1
W(υ2+υ1)υ1V1+υ2V2
W(υ2−υ1)υ1V2−υ2V1
W(υ2−υ1)υ1V2−υ1V1
The correct Answer is:C
Using Einstein.s equation, hυ=W+eV0
When the incident light frequency is υ2 then stopping potential is V2
∴hυ2=W+eV2
from eqns. (i) and (ii) , υ1υ2=W+eV1W+eV2
On solving Wυ1+eV2υ1=Wυ2+eV1υ2
⇒e=W(uψlo2−υ1)υ1V2−υ2V1
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS15videos
PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISM
- BOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))2videos
OSCILLATIONS AND WAVES
- BOOK - MTG-WBJEECHAPTER - SOLID STATE ELECTRONS EXERCISE - WB JEE Previous Years Questions (CATEGORY 1 : Single Option Correct Type)15videos
SOLID STATE ELECTRONS
Similar Questions
Find the frequency of light incident on a metal surface if the photocurrent is brought to zero by a stopping potential of 2.6V. The threshold frequency for the metal surface is 5×1014/s .
View SolutionWhen light off frequency v1 is incident on a photosensitive surface , the stopping potential is V1 . If the frequency of incident radiation becomes v1/2 the stopping potential changes to V2 Find out the expression for the threshold frequency for the surface in terms of V1andV2
If the frequency of incident radiation is doubled , will the maximum kinetic energy of the photoelectrons also be doubled ? Given reason .View Solution
Knowledge Check
- Question 1 - Select One
When light of wavelenght λ incident on a metal then stopping potential is 10V. If wavelengt is increase to 3λ then stopping potential is 2V . Which of the following can emit electron form the metal : -
A5λB7λC9λD10λ - Question 2 - Select One
The figure showing the correct relationship between the stopping potential V and the frequency v of the light for potassium and tungsten is
A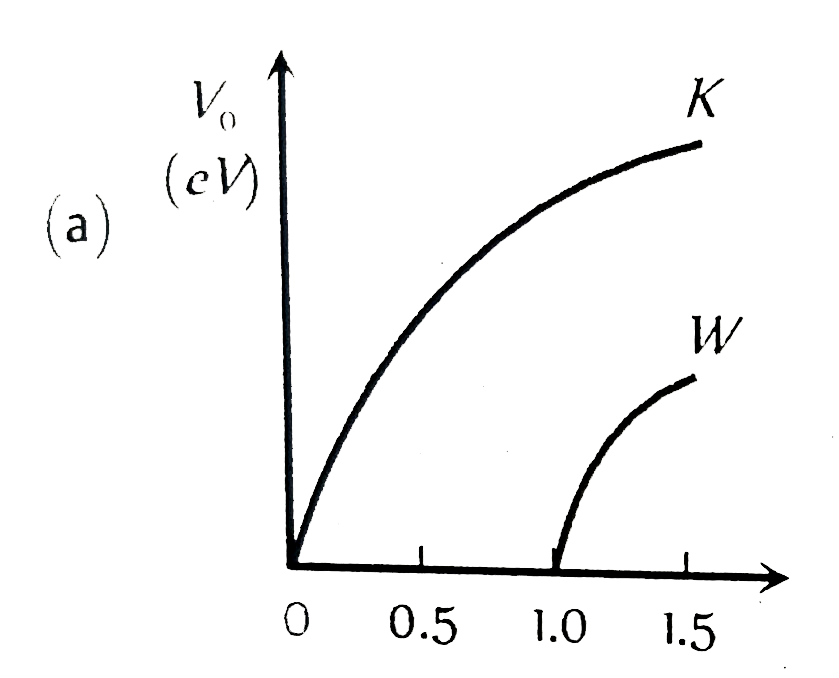 B
B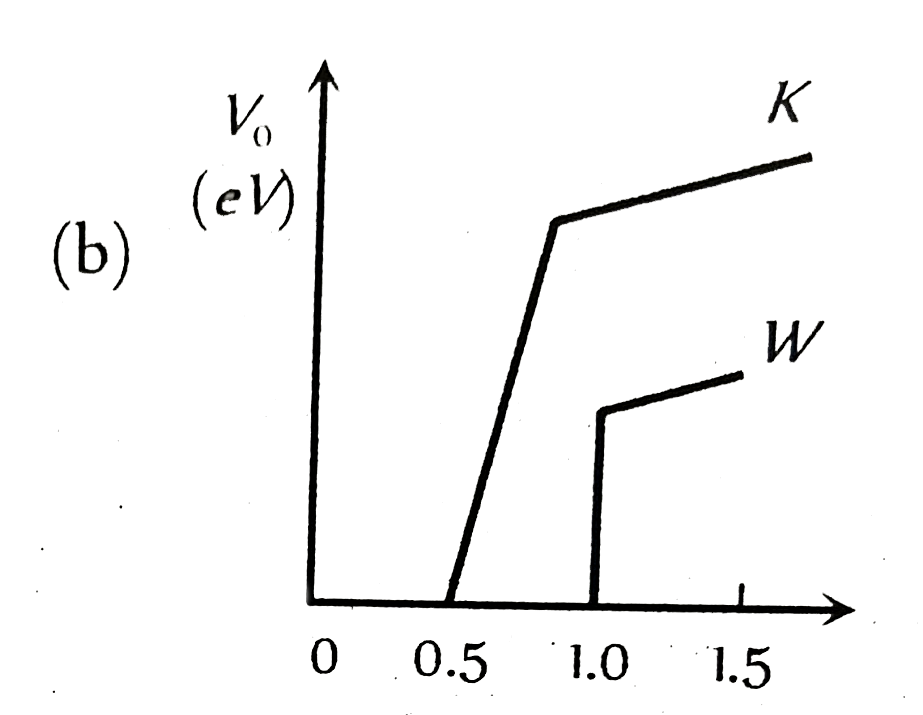 C
C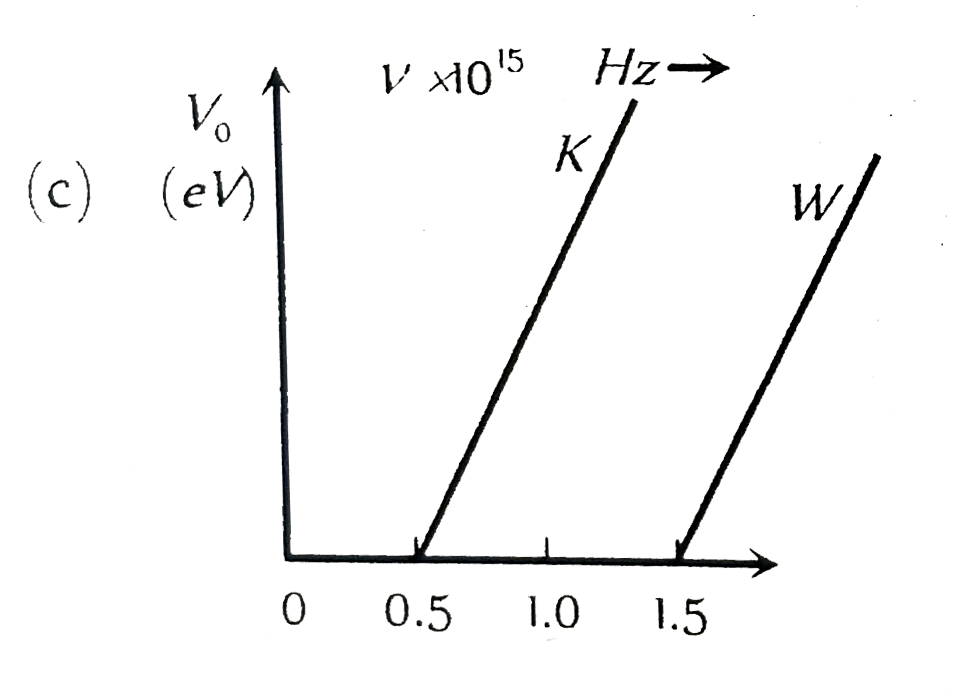 D
D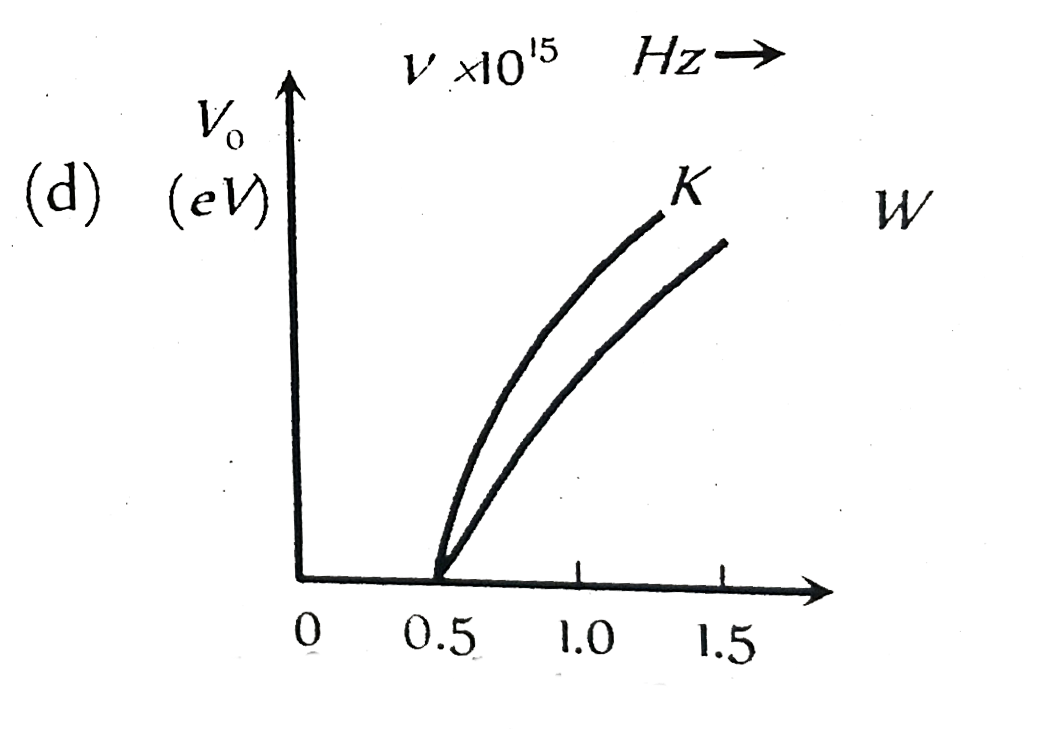
- Question 3 - Select One
Choose the graph showing the correct relationship between the stopping potential V0 and the frequency v of light for potassium and tungsten.
A B
B C
C D
D
The frequency (v) of the incident radiation is greater than threshold frequency v0 in photocell. How will the stopping potential very if frequency v is increased, keeping other factors constant.
View SolutionWhen ultraviolet radiation of a certain frequency falls on a potassium target, the photoelectrons released can be stopped completely by a retarding potential of 0.6 V. If the frequency of the radiation is increased by 10%, this stopping potential rises to 0.9 V. The work function of potassium is
View SolutionWhen ultraviolet radiation of a certain frequency falls on a potassium target, the photoelectrons released can be stopped completely by a retarding potential of 0.5 V. If the frequency of the radiation is increased by 10 %, this stopping potential rises to 0.9 V. The work function of potassium is
View SolutionWhich of the following is the graph between the frequency (v) of the incident radiations and the stopping potential ?
View SolutionFor intensity I of a light of wavelength 5000Å the photoelectron saturation current is 0.40μA and stopping potential is 1.36V , the work function of metal is
View Solution

