when two displacements represented by $y_{1} = a sin (ω t)$ and $y_{2} = b cos (ω t)$ are superimposed the motion is

A

Not a simple harmonic

B

Simple harmonic with amplitude $\frac{a}{b}$

C

Simple harmonic with amplitude ${\sqrt{a}}^{2} + b^{2}$

D

Simple harmonic with amplitude $\frac{(a) + (b)}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

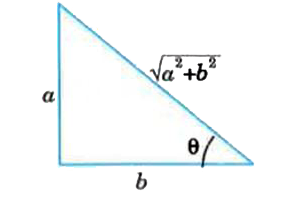
$y = y_{1} + y_{2}$
$= a sin ω t + b cos ω t$
$= \sqrt{a^{2} + b^{2}} (\frac{a}{\sqrt{(a^{2} + b^{2})}} sin ω t + \frac{b}{\sqrt{a^{(2)} + b^{2}}} cos ω t)$
$= \sqrt{a^{2} + b^{2}} [cos θ sin ω t + sin θ cos ω t]$
$= \sqrt{a^{2} + b^{2}} sin (ω t + θ)$
$y = A sin (ω t + θ)$
It executes S.H.M. with amplitude $\sqrt{a^{2} + b^{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
When two displacement represented by $y_{1} = a sin (ω t)$ and $y_{2} = b cos (ω t)$ are superimposed, the motion is
Anot a simple harmonic
Bsimple harmonic with amplitude $\frac{a}{b}$
Csimple harmonic with amplitude $\sqrt{a^{2} + b^{2}}$
Dsimple harmonic with amplitude $\frac{(a^{2} + b^{2})}{2}$
Question 2 - Select One
Two wave are represented by equation $y_{1} = a sin ω t$ and $y_{2} = a cos ω t$ the first wave :-
Aleads the second by $π$
Blags the second by $π$
Cleads the second by $\frac{π}{2}$
Dlags the second by $\frac{π}{2}$
Question 3 - Select One
Two waves represented by $y_{1} = a sin ω t and y_{2} = a sin (ω t + ϕ) with ϕ = \frac{π}{2}$
are superposed at any point at a particular instant. The resultant amplitude is
Aa
B4a
C $\sqrt{2 a}$
Dzero

MODERN PUBLICATION-OSCILLATIONS -Competition File (Multiple choice questions) AIPMT/NEET other State Boards for Medical Entrance

Home
Ask Doubt
Profile