Which arrangement of 3Ω resistors will give a total resistance of 7Ω?
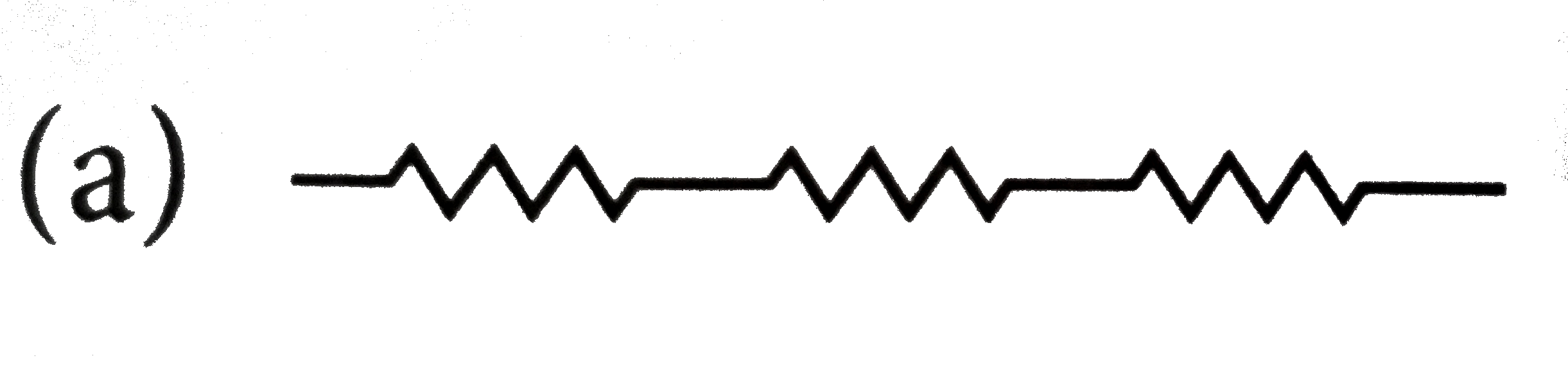
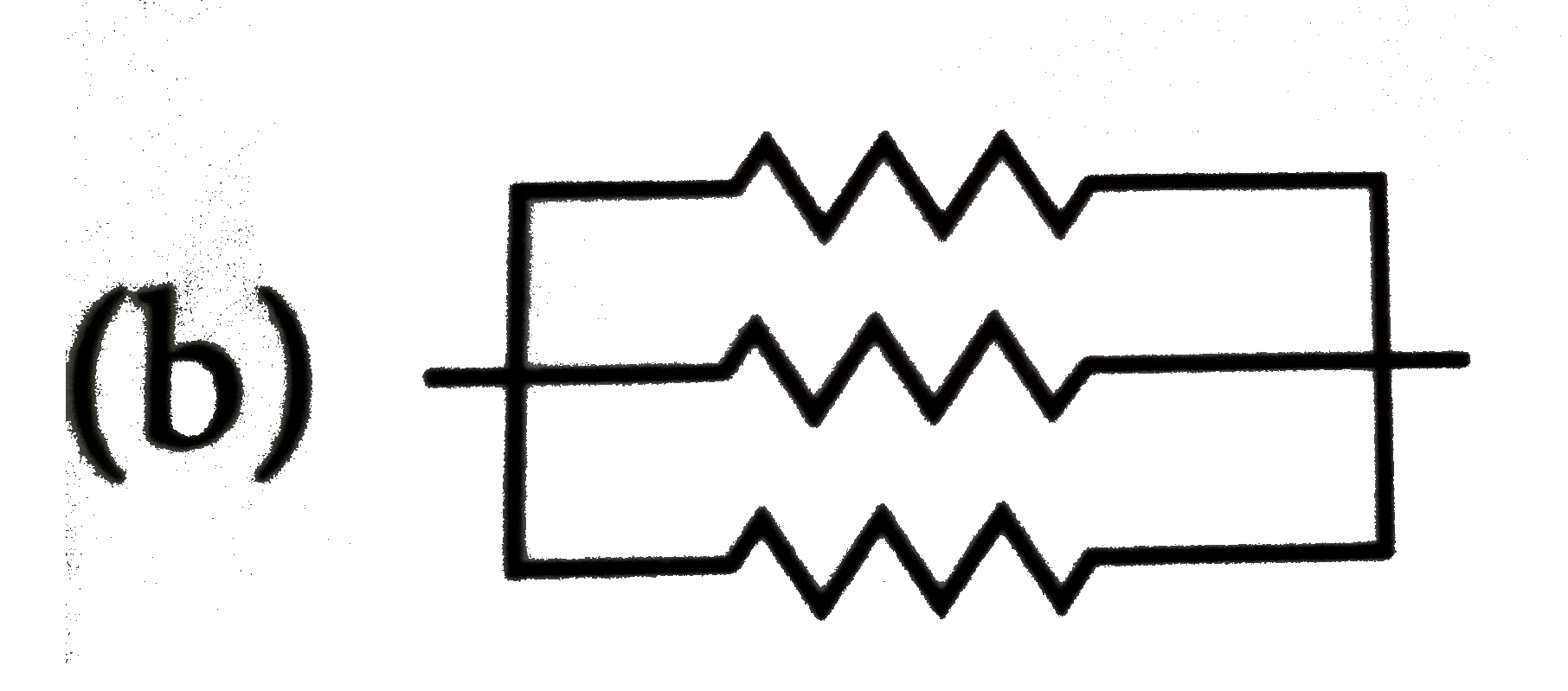

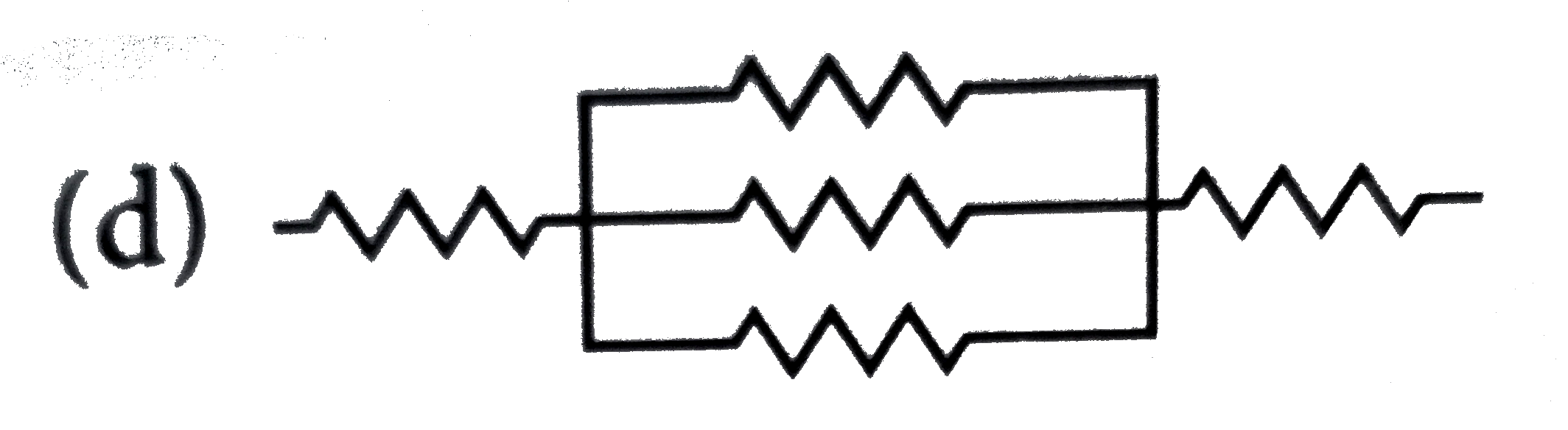
The correct Answer is:D
To find the arrangement of three 3-ohm resistors that results in a total resistance of 7 ohms, we can analyze the different configurations of resistors: series and parallel.
1. Series Connection:
- When resistors are connected in series, the total resistance (R_s) is the sum of the individual resistances.
- For three 3-ohm resistors in series:
Rs=R1+R2+R3=3Ω+3Ω+3Ω=9Ω
- This configuration gives us 9 ohms, which is not the required 7 ohms.
Hint: Remember that in a series connection, the total resistance is simply the sum of all resistances.
2. Parallel Connection:
- When resistors are connected in parallel, the total resistance (R_p) can be calculated using the formula:
1Rp=1R1+1R2+1R3
- For three 3-ohm resistors in parallel:
1Rp=13+13+13=1⟹Rp=1Ω
- This configuration gives us 1 ohm, which is also not the required 7 ohms.
Hint: In a parallel connection, the total resistance is less than the smallest individual resistance.
3. Combination of Series and Parallel:
- Now, let's consider a combination where one resistor is in series with two resistors in parallel.
- Let’s take one 3-ohm resistor in series with two 3-ohm resistors connected in parallel.
- First, calculate the equivalent resistance of the two parallel resistors:
1Rparallel=13+13=23⟹Rparallel=32=1.5Ω
- Now, add this result to the resistance of the series resistor:
Rtotal=Rseries+Rparallel=3Ω+1.5Ω=4.5Ω
- This configuration gives us 4.5 ohms, which is still not 7 ohms.
Hint: When combining resistors, carefully calculate the equivalent resistance for both series and parallel arrangements.
4. Final Configuration:
- Now, let’s try connecting one 3-ohm resistor in series with a parallel combination of three 3-ohm resistors.
- First, calculate the total resistance of the three resistors in parallel:
1Rparallel=13+13+13=1⟹Rparallel=1Ω
- Now, add this to the resistance of the series resistor:
Rtotal=Rseries+Rparallel=3Ω+1Ω=4Ω
- This configuration gives us 4 ohms, which is still not 7 ohms.
5. Correct Configuration:
- The correct arrangement is one resistor in series with a parallel combination of two resistors.
- One 3-ohm resistor is in series with the equivalent resistance of two 3-ohm resistors in parallel:
Rparallel=1.5Ω(from previous calculation)
- Now, add the series resistor:
Rtotal=3Ω+1.5Ω=4.5Ω
- This configuration gives us 4.5 ohms, which is still not 7 ohms.
6. Final Check:
- The correct arrangement is to have one 3-ohm resistor in series with the parallel combination of the other two 3-ohm resistors:
Rtotal=3Ω+1Ω=4Ω
- This configuration gives us 4 ohms, which is still not 7 ohms.
After checking all configurations, the only way to achieve a total resistance of 7 ohms is to have one 3-ohm resistor in series with the equivalent resistance of three 3-ohm resistors connected in parallel.
Conclusion:
The correct arrangement of three 3-ohm resistors to achieve a total resistance of 7 ohms is to connect one 3-ohm resistor in series with the parallel combination of the other two 3-ohm resistors.
Final Answer: The correct option is D.
- When resistors are connected in series, the total resistance (R_s) is the sum of the individual resistances.
- For three 3-ohm resistors in series:
Rs=R1+R2+R3=3Ω+3Ω+3Ω=9Ω
- This configuration gives us 9 ohms, which is not the required 7 ohms.
- When resistors are connected in parallel, the total resistance (R_p) can be calculated using the formula:
1Rp=1R1+1R2+1R3
- For three 3-ohm resistors in parallel:
1Rp=13+13+13=1⟹Rp=1Ω
- This configuration gives us 1 ohm, which is also not the required 7 ohms.
- Now, let's consider a combination where one resistor is in series with two resistors in parallel.
- Let’s take one 3-ohm resistor in series with two 3-ohm resistors connected in parallel.
- First, calculate the equivalent resistance of the two parallel resistors:
1Rparallel=13+13=23⟹Rparallel=32=1.5Ω
- Now, add this result to the resistance of the series resistor:
Rtotal=Rseries+Rparallel=3Ω+1.5Ω=4.5Ω
- This configuration gives us 4.5 ohms, which is still not 7 ohms.
- Now, let’s try connecting one 3-ohm resistor in series with a parallel combination of three 3-ohm resistors.
- First, calculate the total resistance of the three resistors in parallel:
1Rparallel=13+13+13=1⟹Rparallel=1Ω
- Now, add this to the resistance of the series resistor:
Rtotal=Rseries+Rparallel=3Ω+1Ω=4Ω
- This configuration gives us 4 ohms, which is still not 7 ohms.
- The correct arrangement is one resistor in series with a parallel combination of two resistors.
- One 3-ohm resistor is in series with the equivalent resistance of two 3-ohm resistors in parallel:
Rparallel=1.5Ω(from previous calculation)
- Now, add the series resistor:
Rtotal=3Ω+1.5Ω=4.5Ω
- This configuration gives us 4.5 ohms, which is still not 7 ohms.
- The correct arrangement is to have one 3-ohm resistor in series with the parallel combination of the other two 3-ohm resistors:
Rtotal=3Ω+1Ω=4Ω
- This configuration gives us 4 ohms, which is still not 7 ohms.
The correct arrangement of three 3-ohm resistors to achieve a total resistance of 7 ohms is to connect one 3-ohm resistor in series with the parallel combination of the other two 3-ohm resistors.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - CELLS, EMF, INTERNAL RESISTANCE
6 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - KIRCHOFF S LAW
14 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ELECTRICAL ENERGY, POWER
8 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason
30 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
In which of the follwing arrangements of resistors does the meter M, which has a resistance of 2Ω, give the largest reading when the same potential difference is appliced between points P and Q?
View SolutionHow can three resistors of resistances 2Ω,3Ω, and 6Ω be connected to give a total resistance of
(a) 4Ω
(b) 1Ω ?
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View SolutionThe network shown in figure is an arrangement of nine identical resistors. The resistance of the network between points A and B is 1.5Ω. The resistance r is
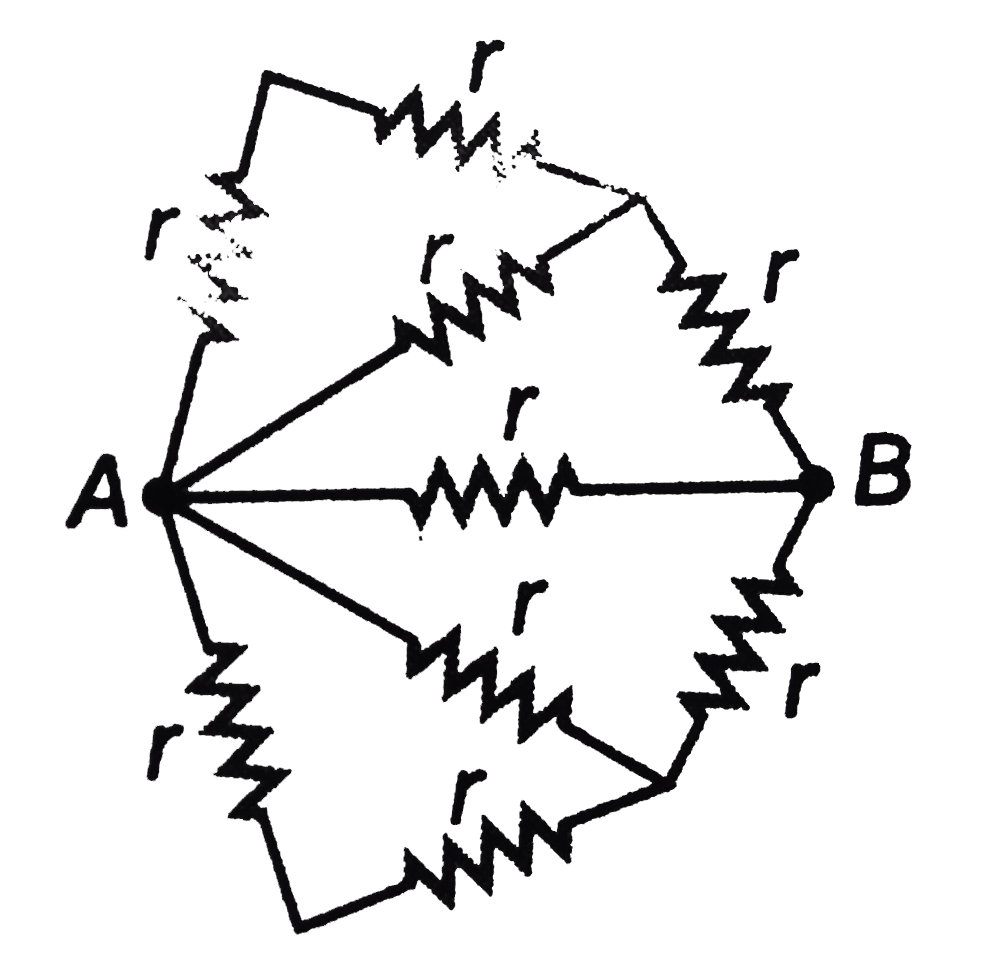
View SolutionA circuit consists of a resistor of 1 ohm in series with a parallel arrangement of resistors of 6 ohm and 3 ohm. Calculate the total resistance of the circuit. Draw a diagram of the arrangment.
View SolutionThree resistors each of 2 Ω are connected together so that their total resistance is 3 Ω. Draw a diagram to show this arrangement and check it by calculation.
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View SolutionFind the current in each resistor of the circuit shown in fig
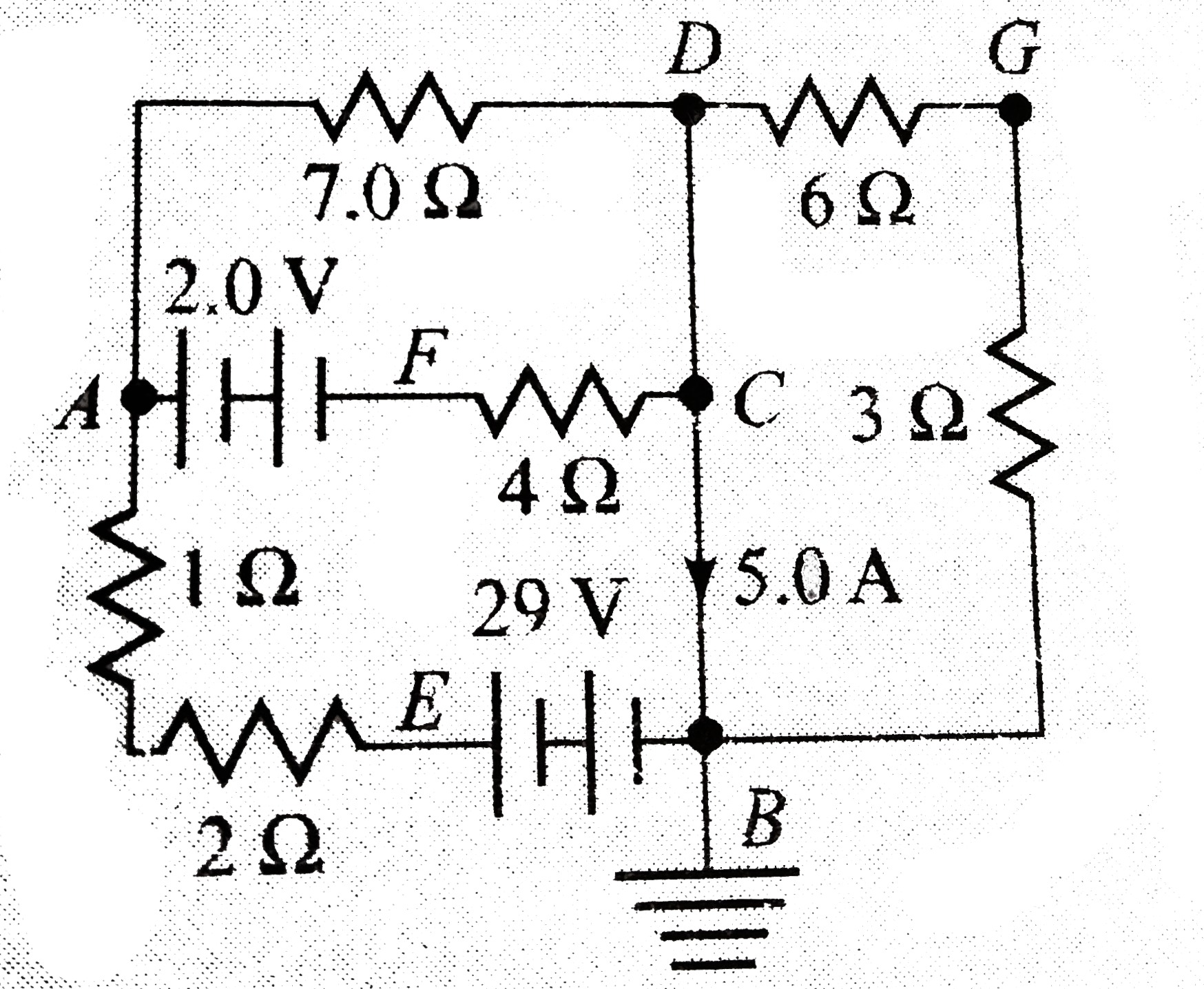
a. Current thorugh resistance of 6Ωis………..
b. Current thorugh resistance of 3Ωis………..
c. Current thorugh resistance of 2Ωis………..
d. Current thorugh resistance of 5Ωis………..
View SolutionYou have three resistors of values 2Ω,3Ωand5Ω. How will you join them so that the total resistance is more than 7Ω?
Draw a diagram for the arrangement.
View SolutionYou have three resistors of values 2Ω,3Ωand5Ω. How will you join them so that the total resistance is more than 7Ω?
Calculate the equivalent resistance.
View Solution
