Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).

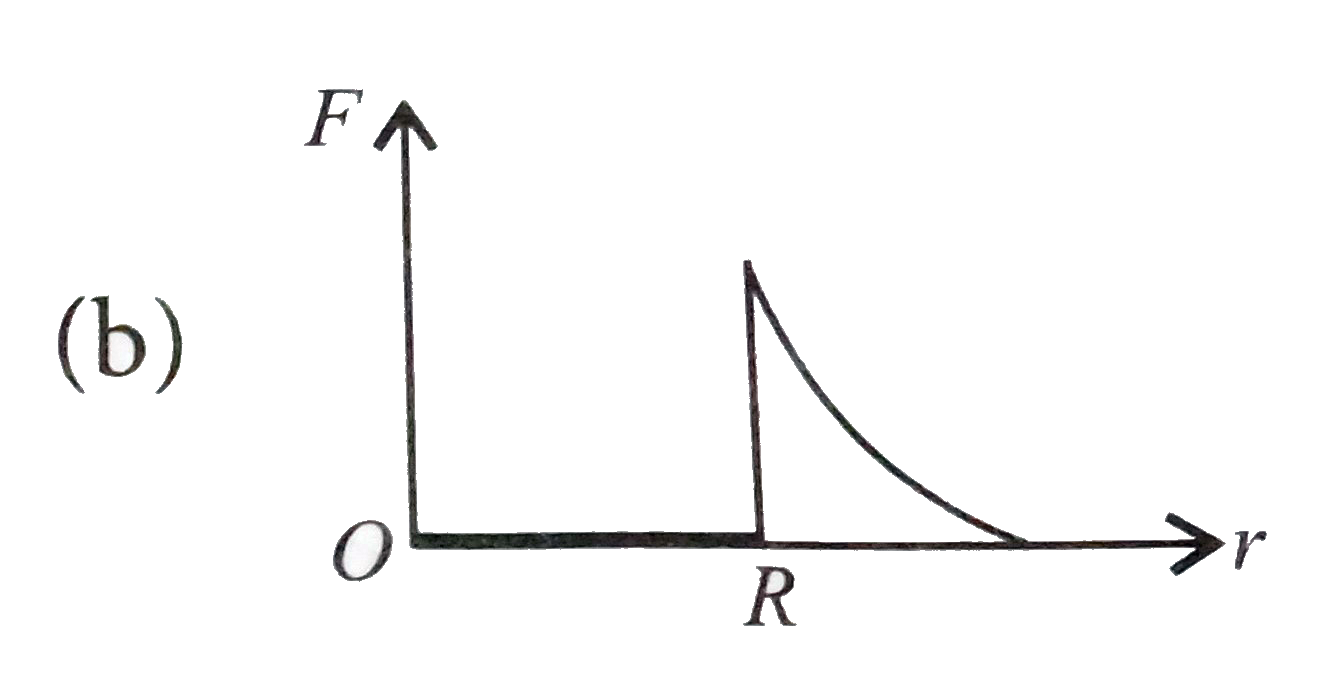
The correct Answer is:B
To determine the variation of the gravitational field E on a particle with distance r due to a thin spherical shell of radius R, we can analyze the gravitational field both inside and outside the shell.
1. Understanding the Setup:
- We have a thin spherical shell with radius R.
- We need to find the gravitational field at a distance r from the center of the shell.
2. Inside the Shell (r<R):
- According to the shell theorem, the gravitational field inside a thin spherical shell is zero.
- Therefore, for any point inside the shell (i.e., r<R), the gravitational field E is:
E=0
3. Outside the Shell (r≥R):
- For points outside the shell, the gravitational field behaves as if all the mass of the shell were concentrated at its center.
- The gravitational field E at a distance r from the center is given by:
E=GMr2
- Here, M is the total mass of the shell, and G is the gravitational constant.
4. Graphing the Gravitational Field:
- For r<R: The gravitational field E=0.
- For r=R: The gravitational field starts to decrease as 1r2.
- For r>R: The gravitational field decreases inversely with the square of the distance.
5. Conclusion:
- The graph of the gravitational field E versus distance r will be zero for r<R and will decrease as 1r2 for r≥R.
- Thus, the correct plot representing this variation is option B.
- We have a thin spherical shell with radius R.
- We need to find the gravitational field at a distance r from the center of the shell.
- According to the shell theorem, the gravitational field inside a thin spherical shell is zero.
- Therefore, for any point inside the shell (i.e., r<R), the gravitational field E is:
E=0
- For points outside the shell, the gravitational field behaves as if all the mass of the shell were concentrated at its center.
- The gravitational field E at a distance r from the center is given by:
E=GMr2
- Here, M is the total mass of the shell, and G is the gravitational constant.
- For r<R: The gravitational field E=0.
- For r=R: The gravitational field starts to decrease as 1r2.
- For r>R: The gravitational field decreases inversely with the square of the distance.
- The graph of the gravitational field E versus distance r will be zero for r<R and will decrease as 1r2 for r≥R.
- Thus, the correct plot representing this variation is option B.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - HOTS10videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - NCERT Exemplear Problems.8videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Weightlessness2videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
Similar Questions
Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionFollowing curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
 View Solution
View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
 View Solution
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionIntensity of gravitational field inside the hollow spherical shell is
View SolutionA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
View Solution

