While stating Boyle's law why should we use the phrase " at constant temperature"?
Step-by-Step Solution:
1. Understanding Boyle's Law: Boyle's Law states that for a given mass of gas at constant temperature, the pressure (P) of the gas is inversely proportional to its volume (V). This can be mathematically expressed as PV=k, where k is a constant.
2. Importance of Constant Temperature: The phrase "at constant temperature" is crucial because the behavior of gas particles is influenced by temperature. Temperature is a measure of the average kinetic energy of the gas particles. If the temperature changes, the kinetic energy of the particles changes, which affects the pressure and volume relationship.
3. Kinetic Energy and Particle Motion: When gas particles are heated (increased temperature), they move faster and collide with the walls of the container more frequently and with greater force. This results in an increase in pressure. Conversely, if the gas is cooled (decreased temperature), the particles move slower, collide less frequently, and the pressure decreases.
4. Implication of Changing Temperature: If we do not keep the temperature constant while changing the volume of the gas, the pressure will not solely depend on the volume. Instead, it will also be affected by the temperature change, leading to a misunderstanding of the relationship described by Boyle's Law.
5. Conclusion: Therefore, to accurately state Boyle's Law and observe the inverse relationship between pressure and volume, it is essential to maintain a constant temperature. This ensures that any changes in pressure or volume are solely due to the changes in volume or pressure, respectively, without the confounding effects of temperature variations.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (KINETIC THEORY OF GASES ) VERY SHORT ANSWER QUESTIONS
11 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (KINETIC THEORY OF GASES ) FROM GAS LAW AND EQUATION OF STATE
12 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (KINETIC THEORY OF GASES ) LONG ANSWER QUESTIONS
9 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
Knowledge Check
Which law states that "product of volume and pressure at constant temperature is constant for a dry gas of given mass".
ACharles.s lawBBoyle.s lawCHenry.s lawDDalton.s law
Boyle's law states that when a sample of gas is compressed at a constant temperature , the pressure of the gas is inversely proportional to the volume of the gas . If a sample of air occupies 0.106m3 at 25∘C , the pressure is 50 kPa (kilopascals). Find the new pressure , in kPa, if the temperature remains constant and the sample expands to a volume of 0.3m3.
View SolutionWhy should we not eat polished rice?
View SolutionWhy should we conserve forests and wildlife?
View SolutionThe graph betwene P and V at constant temperature should look like
View SolutionFor Boyle's law to be hold good, the gas should be
View SolutionSketch shows the plot of Z v/s P for a hypothetical gas for one mole at three distint temperature.
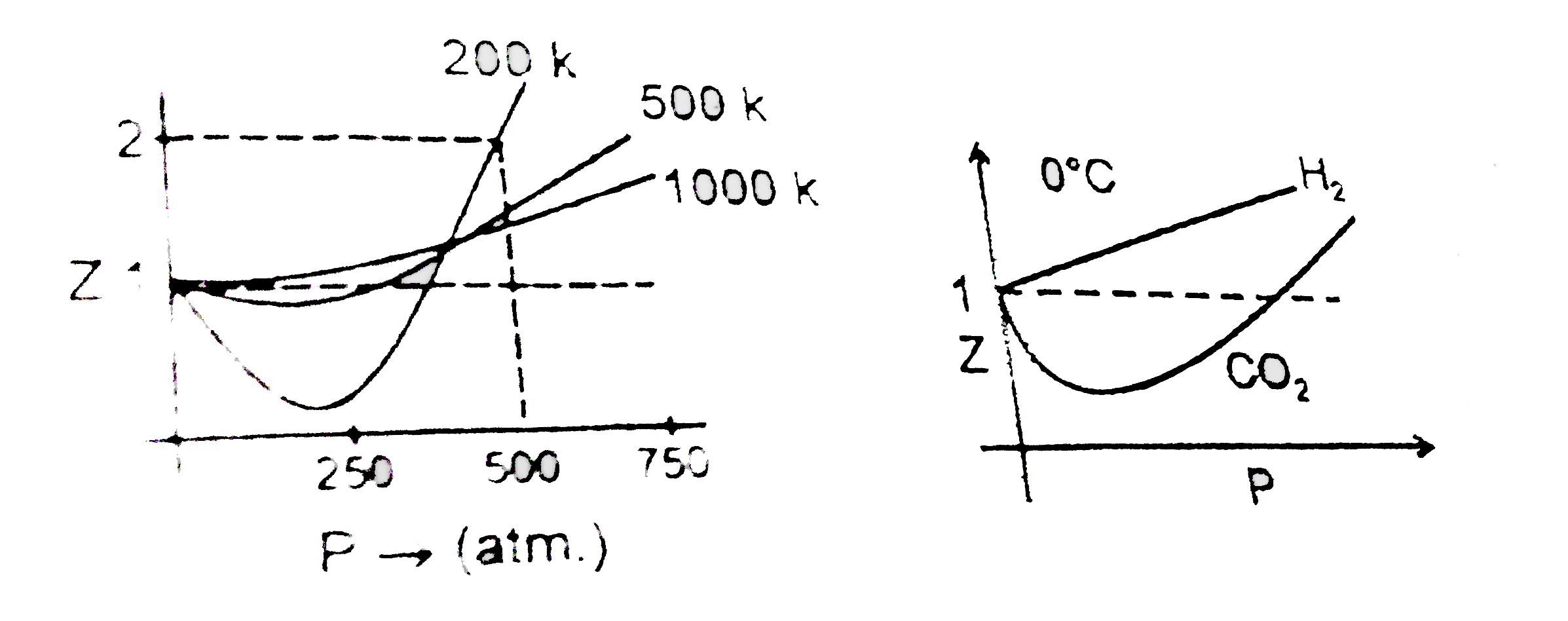
Boyle's temperature is the temperature at which gas shows ideal behaviour over a pressure range in the low pressure region.Boyle's temperature (Tb)=aRb.If a plot is obtained at temperature well below Boyle's temperature then the curve will show negative deviation, in low pressure region and positive deviation in the high pressure region. Near critical temperature the curve is more likely as CO2 and the temperature well above critical temperature curve is more like H2 at 0∘C as shown above.At high pressure suppose all the constant temperature curve varies linearly with pressure according to the following equation : Z=1+PbRT (R=2calmol−1K−1)
Which of the following is correct :
View SolutionWe write the relation for Boyle's law in the form, PV=KB when the temperature remains constant. In this relation, the magnitude of KB depends upon the
View Solution
