White light reflected from a soap film (Refractive index =1.5 ) has a maxima at 600 nm and a minima at 450 nm at with no minimum in between. Then, the thickness of the film is
1 micro meter
2 micro meter
3 micro meter
4 micro meter
The correct Answer is:C
To solve the problem of finding the thickness of a soap film given the maxima and minima of reflected white light, we can follow these steps:
Step 1: Understand the Conditions for Maxima and Minima
For a soap film with a refractive index μ=1.5:
- The condition for maxima (constructive interference) is given by:
2μtcosr=(2n+1)λ12
- The condition for minima (destructive interference) is given by:
2μtcosr=nλ2
Where:
- t is the thickness of the film,
- r is the angle of refraction (which we can assume to be 0 for normal incidence, making cosr=1),
- λ1=600nm (for maxima),
- λ2=450nm (for minima),
- n is an integer representing the order of interference.
Step 2: Set Up the Equations
Using the values given:
1. For maxima at λ1=600nm:
2×1.5×t=(2n+1)600nm2
Simplifying this gives:
3t=(2n+1)×300
(Equation 1)
2. For minima at λ2=450nm:
2×1.5×t=n×450nm
Simplifying this gives:
3t=450n
(Equation 2)
Step 3: Divide the Equations
Now, we can divide Equation 1 by Equation 2 to eliminate t:
(2n+1)×300450n=1
Cross-multiplying gives:
(2n+1)×300=450n
Expanding this:
600n+300=450n
Rearranging gives:
600n−450n=−300
150n=−300
n=2
Step 4: Substitute Back to Find Thickness
Now that we have n=2, we can substitute this back into either Equation 1 or Equation 2 to find t. Using Equation 1:
3t=(2×2+1)×300
3t=(4+1)×300
3t=5×300
3t=1500
t=15003=500nm
Final Result
Thus, the thickness of the soap film is:
t=500nmor5×10−7m
For a soap film with a refractive index μ=1.5:
- The condition for maxima (constructive interference) is given by:
2μtcosr=(2n+1)λ12
- The condition for minima (destructive interference) is given by:
2μtcosr=nλ2
- t is the thickness of the film,
- r is the angle of refraction (which we can assume to be 0 for normal incidence, making cosr=1),
- λ1=600nm (for maxima),
- λ2=450nm (for minima),
- n is an integer representing the order of interference.
Using the values given:
1. For maxima at λ1=600nm:
2×1.5×t=(2n+1)600nm2
Simplifying this gives:
3t=(2n+1)×300
(Equation 1)
2×1.5×t=n×450nm
Simplifying this gives:
3t=450n
(Equation 2)
Now, we can divide Equation 1 by Equation 2 to eliminate t:
(2n+1)×300450n=1
Cross-multiplying gives:
(2n+1)×300=450n
Expanding this:
600n+300=450n
Rearranging gives:
600n−450n=−300
150n=−300
n=2
Now that we have n=2, we can substitute this back into either Equation 1 or Equation 2 to find t. Using Equation 1:
3t=(2×2+1)×300
3t=(4+1)×300
3t=5×300
3t=1500
t=15003=500nm
Thus, the thickness of the soap film is:
t=500nmor5×10−7m
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE main (Only one option is Correct )
22 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced Only one option is correct
22 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - match column
4 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
White light reflected at normal incidence from a soap film has minima at 6500Å and maxima at 7500Å in the visible region without minimum in between. If μ is 53 for the thin film, thickness of the film is
View SolutionA parallel beam of white light falls on a thin film whose refractive index is equal to 4/3. The angle of incidence i=53∘. What must be the minimum film thickness if the reflected light is to be coloured yellow most intensively? (tan53∘=4/3)
View SolutionA parallel beam of white light falls on a thin film whose refractive index is equal to 4/3. The angle of incidence i=53∘. What must be the minimum film thickness if the reflected light is to be coloured yellow most intensively? (tan53∘=4/3)
View SolutionWhen the plastic thin film of refractive index 1.45is placed in the path of one of the interfering waves then the central fringe is displaced through width of five fringes.The thickness of the film will be ,if the wavelength of light is5890Å
View SolutionThe central fringe shifts to the position of fifth bright fringe, if a thin film of refractive index 1.5 is introduced in the path of light of wavelength 5000Å. The thickness of the glass plate is
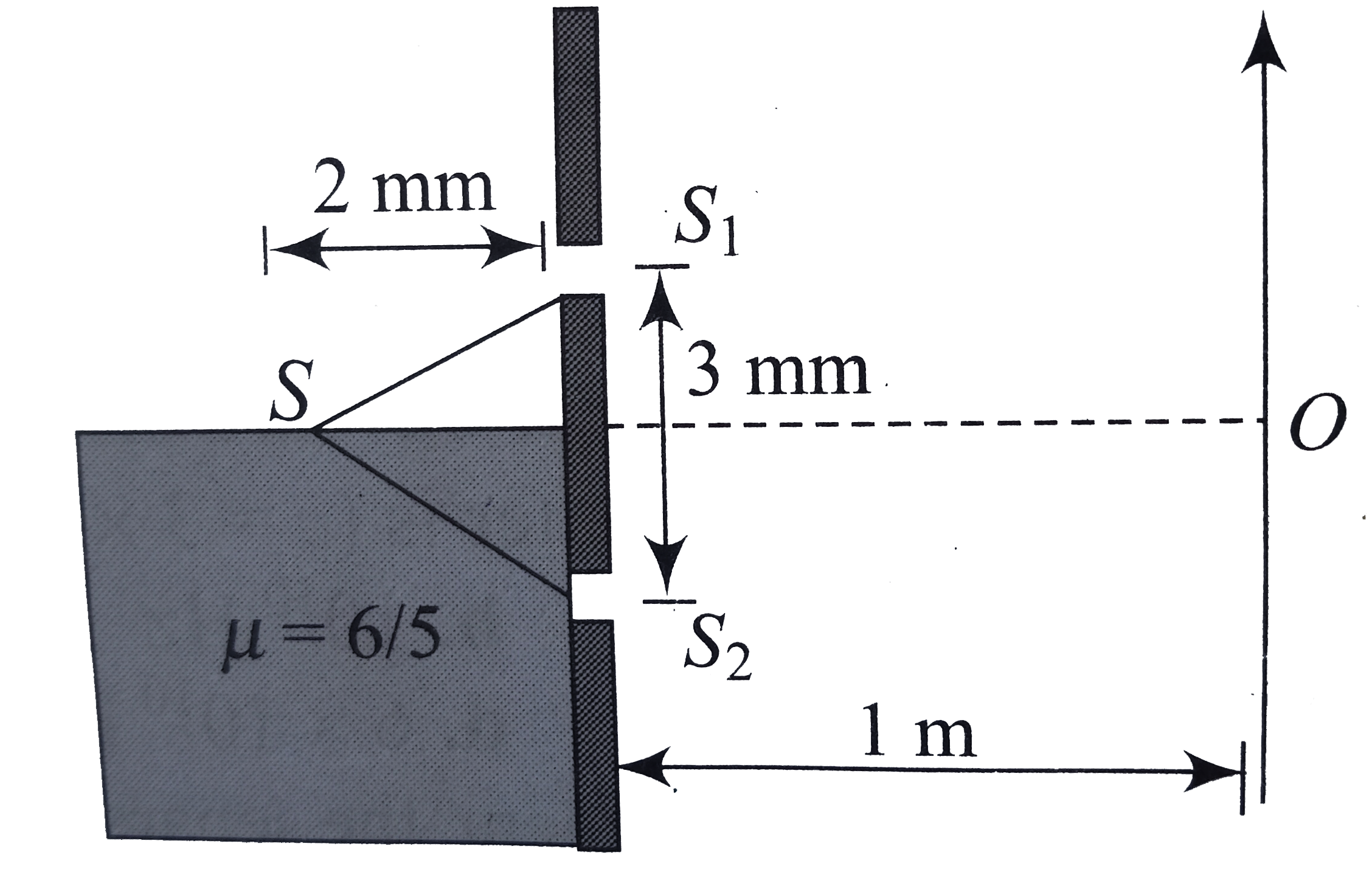
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distacne from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View SolutionTwo slits S1 and S2 illuminated by a white light source give a white central maxima. A transparent sheet of refractive index 1.25 and thickness t1 is placed in front of S1. Another transparent sheet of refractive index 1.50 and thickness t2 is placed in front of S2. If central maxima is not effected, then ratio of the thickness of the two sheets will be :
View Solution
