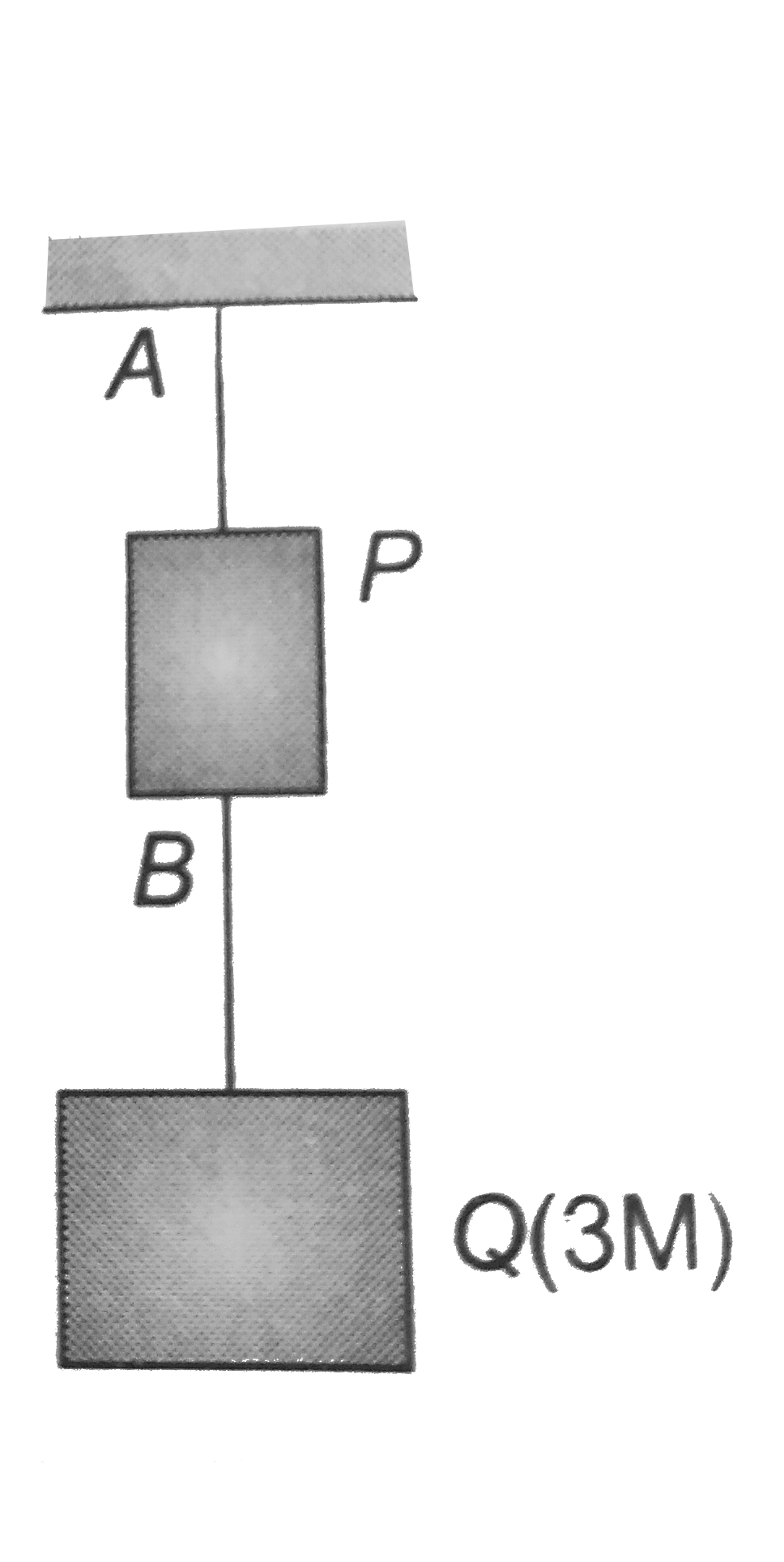
Wires A and B are connected with blocks P and Q, as shown, the ratio of lengths radii and Young's modulus of wires A and B are r, 2r and 3r respectively (r is a constant). Find the mass of block P if ratio of increase in their corresponding length is . The mass of the block Q is 3M
M
3M
6M
9M
The correct Answer is:B
(given)
Mass of block
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Assertion Reasoning20videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - NEET Questions17videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Viscosity29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
Similar Questions
If the ratio of lengths, radii and young's modulii of steel and brass wires in the figure are a,b and c, respectively. Then, the corresponding ratio of increase in their lengths would be
 View Solution
View SolutionIf the ratio of diameter, lengths and Young's modulus of steel and brass wires shown in figure are 2 : 1, 2 : 1 and 2 : 1 respectively, then the corresponding ratio of increase in their lengths would be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c respectively then the corresponding ratio of increase in their lengths is
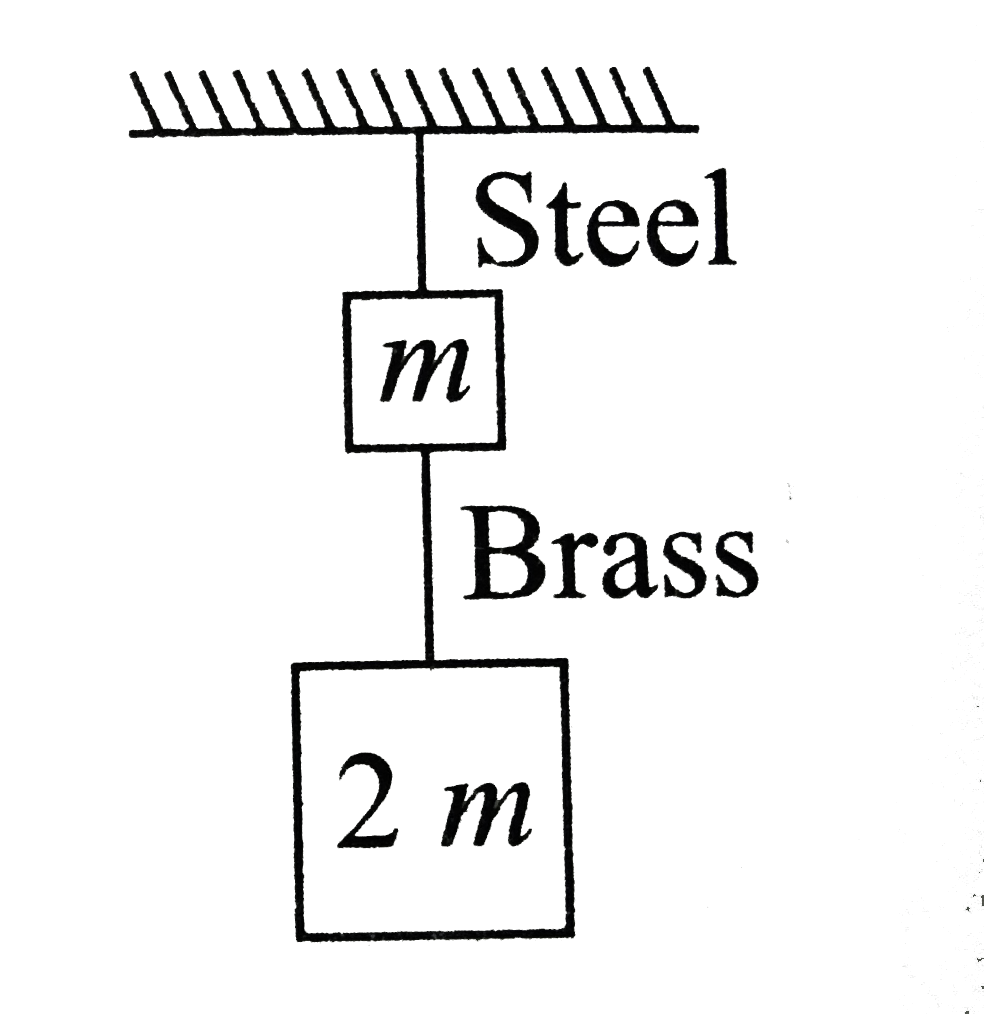 A2a2cbB3a2b2cC2acb2D3c2ab2
A2a2cbB3a2b2cC2acb2D3c2ab2 - Question 2 - Select One
If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c repectively then the corresponding ratio of increase in their lengths is
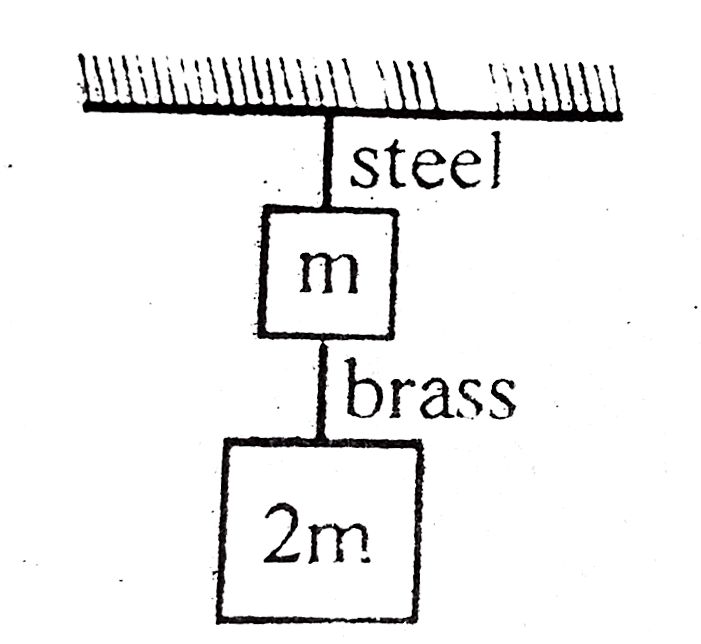 A2a2c/bB3a/2b2cC2ac/b2D3c/2ab2
A2a2c/bB3a/2b2cC2ac/b2D3c/2ab2 - Question 3 - Select One
If the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be
 A3q5p2rB5q3p2rC3q5prD5q3pr
A3q5p2rB5q3p2rC3q5prD5q3pr
If the ratio of lengths, radii and youngs's modulus of steel and and brass wires in figure are 2:1,2:1,3:1 respectively. Then corresponding ratio of increases in their would be. (Neglect the mass of the wire and take g=10m/s2)
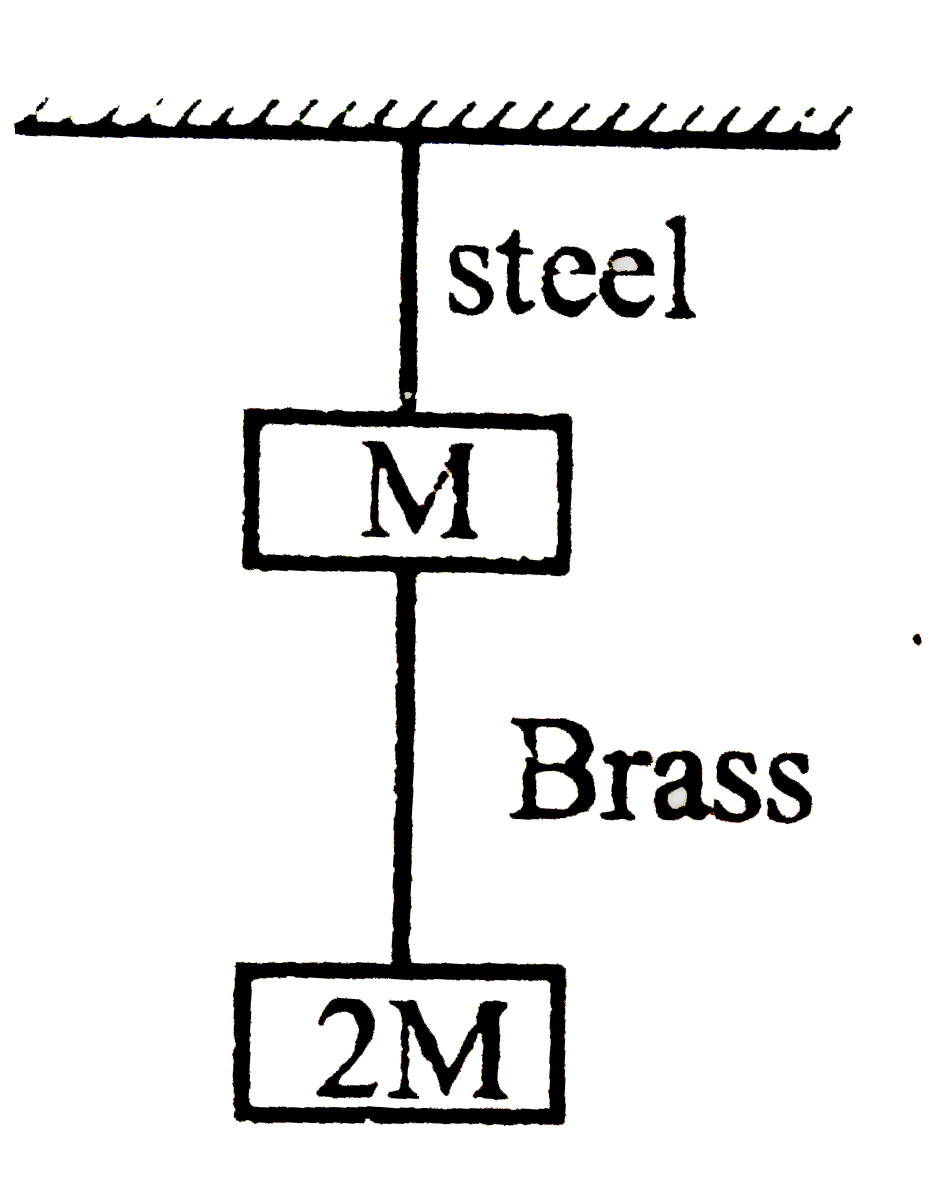 View Solution
View SolutionTwo copper wire of length l and 2l have radii, r and 2r respectively. What si the ratio of their specific resistance.?
View SolutionTwo copper wires of length l and 2l have radii r and 2r respectively. What is ratio of their specific resistances ?
View SolutionTwo copper wires of length l and 2l have radii r and 2r respectively. What is ratio of their specific resistances ?
View SolutionTwo copper wire of length l and 2l have radii, r and 2r respectively. What si the ratio of their specific resistance.?
View Solution

