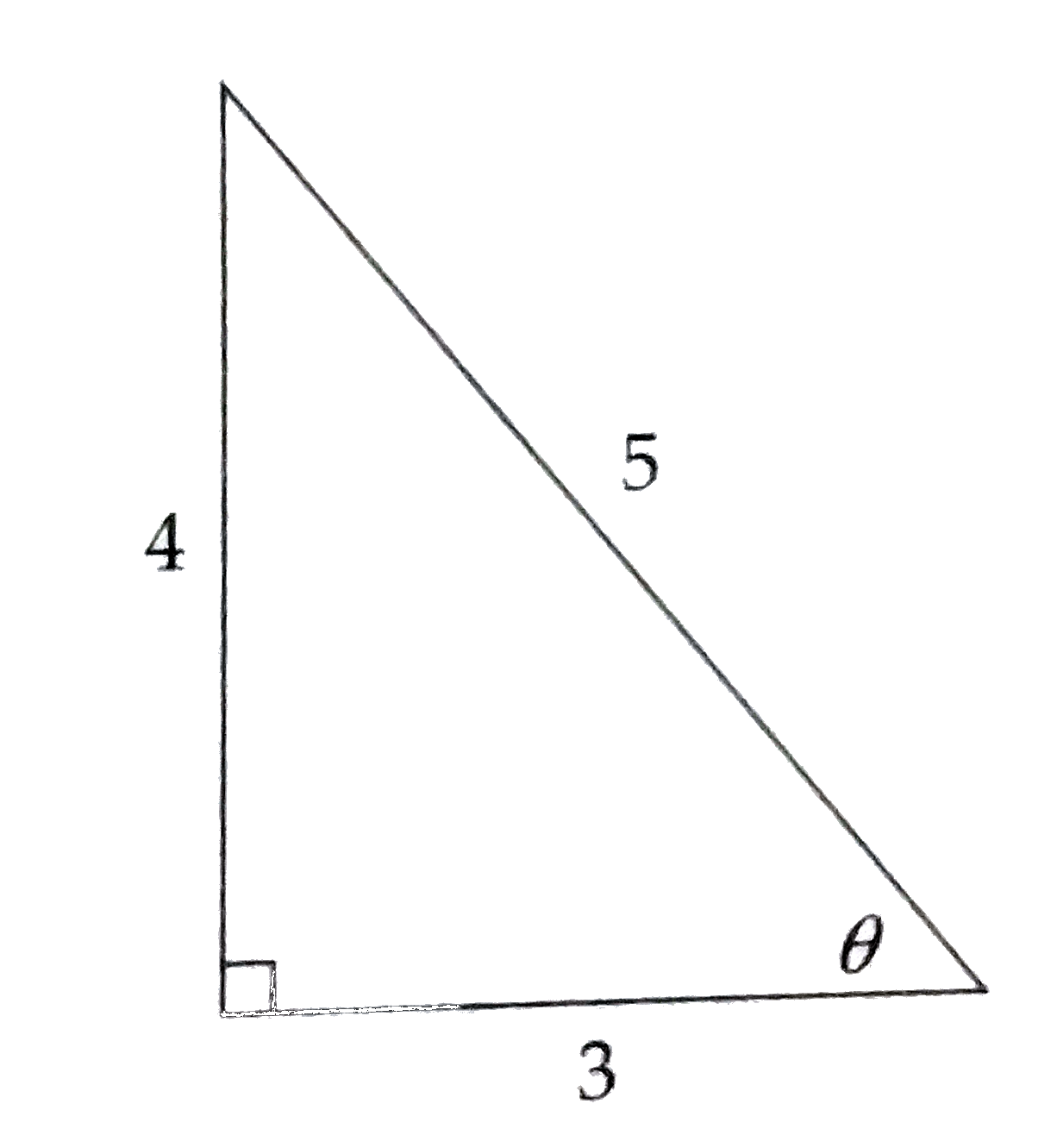
1sinθ+1cosθ=
A
0.75
B
1.20
C
1.43
D
2.92
Video Solution
Text Solution
The correct Answer is:D
Since is opposite over hypotenuse and cosine is adjacent over hypotenuse, so sinθ=45 and cosθ=35. Therefore,
1sinθ+1cosθ=54+53≈1.25+1.67=2.92
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Prove that cosθ1−sinθ+1−sinθcosθ=2secθ.
View SolutionProve that:
(a) sin2θ1+cos2θ=tanθ (b) 1+sin2θ+cos2θ1+sin2θ−cos2θ=cotθView SolutionFind the number points where f(θ)=∫1−1sinθdx1−2xcosθ+x2 is discontinous where θ∈[0,2π].
View SolutionProve that : sinθ−cosθ+1sinθ+cosθ−1=1secθ−tanθ
View SolutionProve that : 1+sinθ−cosθ1+sinθ+cosθ=tan(θ2)
View SolutionProve :cosθ1+sinθ+cosθ1−sinθ=2secθ
View SolutionIf cosθ1cosθ2+sinθ1sinθ2=cosθ0cosθ2+sinθ0sinθ2=1, where θ1 and θ0 do not differ by can even multiple of π, prove that
cosθ1⋅cosθ0cos2θ2+sinθ1⋅sinθ0sin2θ2=−1View SolutionProve that : cosθ1−tanθ+sinθ1−cotθ=sinθ+cosθ
View SolutionSolve 3sinθ−sin3θsinθ+cos3θcosθ=1.
View SolutionIf 0≤θ≤πand81sin2θ+81cos2θ=30 is
View Solution

