A, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
Given: AB=CD
Solution: As we know that equal chords cut off equal arcs in equal circles.
So, AB=CD
AB+BC=BC+CD
arc ABC=arc BCD
chord AC=chord BD
∴ AC=BD Hence proved.
Topper's Solved these Questions
Similar Questions
A, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
 View Solution
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(EBG)=ar(EFC)
View SolutionLet A,B,C,D be four concyclic points in order in which AD:AB=CD:CB. If A,B,C are repreented by complex numbers a,b,c representively, find the complex number associated with point D.
View SolutionAB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
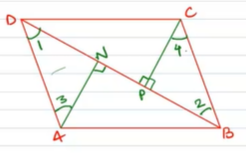 View Solution
View Solution

