ABC is a right triangle right-angled at C . Let BC=a, CA=b, AB=c and let p be the length of perpendicular from C on AB , prove that (i) cp=ab (ii) 1p2=1a2+1b2
(i) We have
ar(ΔABC)=12×12×AB×CD=12cp [ taking BC as base]
∴12cp=12ab⇒cp=ap.
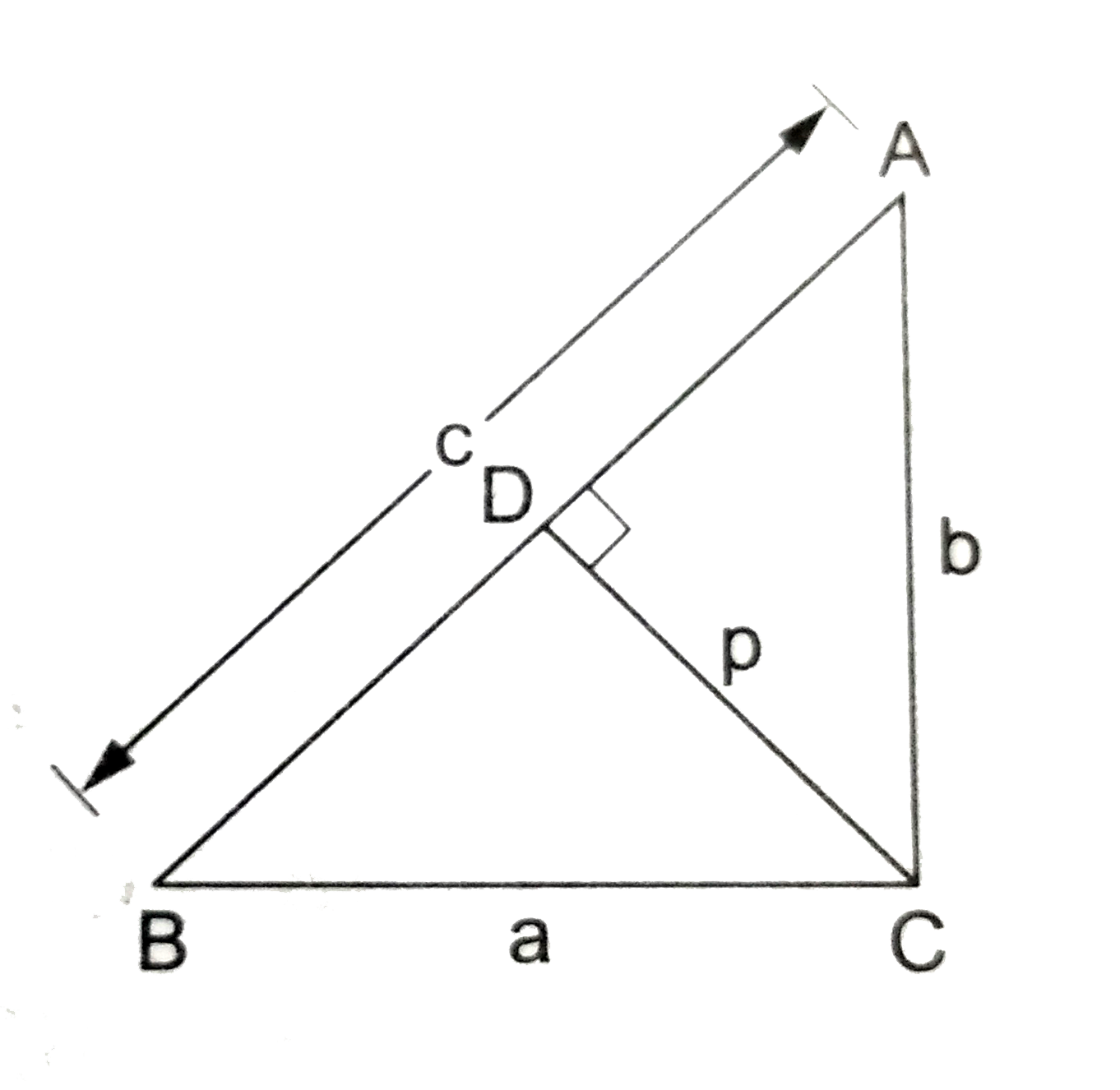
Hence, cp= ab.
(ii)cp=ab⇒1p=cab
∴1p2=c2a2b2=b2+a2a2b2 [∴AB2=AC2+BC2]
=(b2a2b2+a2a2b2)=(1a2+1b2)
Hnece, 1p2=1a2+1b2
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
ABC is a right triangle right-angled at C . Let BC=a, CA=b, AB=c and let p be the length of perpendicular from C on AB , prove that (i) cp=ab (ii) 1p2=1a2+1b2
View SolutionABC is a right triangles right angled at C . Let BC =a ,CA=b, AB = c, and p be the length of perpendicular from C to AB . Prove that cp = ab .
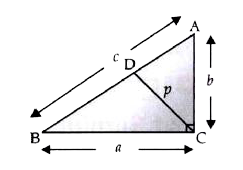
View Solution
Knowledge Check
ABC is a right angled triangle in which ∠C=90∘. If BC=a,AB=c,CA=band the length of perpendicular from C to AB be p. then, 1a2+1b2=?
A1pB2p2C1p2DNone of these
ABC is right angle triangle at C. Let BC = a, CA = b, AB = c and Let 'P' be the length of perpendicular from C to AB. prove that 1p2=1a2+1b2
View SolutionΔABC is a triangle where ∠C=90∘,≤tBC=a,CA=b,AB=c and let 'p' be the length of the perpendicular from C on AB. Prove that: ?
(ii) 1p2=1a2+1b2
View SolutionABC is a right traingle, right angled at C. if P is the length of perpendicular from C to AB and AB=c, BC=a and CA=b, then prove that (i) pc=ab (ii) 1p2=1a2+1b2
View SolutionABC is a triangle right-angled at C. If p is the length of the perpendicular from C to AB and a, b, c are the sides, then which one of the following is correct ?
View SolutionΔABC, is right angles at C. If p is thhe length of the perpendicular from C to AB and a,b,c are the lengths of the sides opposites ∠A,∠B,∠Crespectively then prove that
1p2=1a2+1b2
View SolutionIf a,b,andc are in G.P. then prove that 1a2−b2+1b2=1b2−c2.
View SolutionIf in a right angled triangle, a and b are the lengths of sides and c is the length of hypotenuse and c−b≠1,c+b≠1, then show that
logc+ba+logc−ba=2logc+ba.logc−ba.
View Solution
