ΔABC, is right angles at C. If p is thhe length of the perpendicular from C to AB and a,b,c are the lengths of the sides opposites ∠A,∠B,∠Crespectively then prove that
1p2=1a2+1b2
Step by step video & image solution for DeltaABC , is right angles at C. If p is thhe length of the perpendicular from C to AB and a,b,c are the lengths of the sides opposites angle A,angle B,angle C respectively then prove that 1/(p^(2))=1/(a^(2))+1/(b^(2)) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Long Answer Type Questions )
11 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Multiple Choice Questions)
8 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Multiple Choice Questions)
5 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
Knowledge Check
In a ΔABC right angle at C .P is the length of ⊥ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
A1p2=1b2−1a2B1p2=1a2+1b2C1p2+1a2=−1b2D1p2=1a2−1b2In a ΔABC right angle at C .P is the length of ⊥ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
A1P2=1a2−1b2B1P2=1b2−1a2C1P2=1a2+1b2D1P2+1a2=1b2=0If ΔABC is right angled at C, then the value of cos(A+B) is
A0B1C12D√32
ABC is a triangle right angled at C with BC = a and AC = b. If p is the length of the perpendicular from C on AB, then which one of the following is correct ?
View SolutionABC is a right triangles right angled at C . Let BC =a ,CA=b, AB = c, and p be the length of perpendicular from C to AB . Prove that cp = ab .
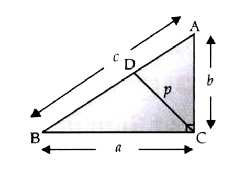
View SolutionΔABC is a triangle where ∠C=90∘,≤tBC=a,CA=b,AB=c and let 'p' be the length of the perpendicular from C on AB. Prove that:
cp=ab
View SolutionIn an equilateral △ABC, if a, b and c denote the lengths of perpendiculars from A, B and C respectively on the opposite sides, then :
View SolutionIf ΔABC is a right-angled at A, then: cos2B+cos2C=
View Solution
