(a) Can the graph of the function intersect the horizontal asymptote?
(b) Can the graph of the function intersect the vertical asymptote?Solution in Bengali
(a) Yes. See the following graph for illustration.

(b) No. If the fraph of the curve intersects the vertical asymptote, then it is not a function as it fails the vertical line test.

Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.11
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.12
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.9
1 Videos
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
The graph of y = f(x) is given with six labelled points. Anser the following questions.
(a) At which point f'(x) has the greatest value?
(b) At which point f(x) and f'(x) both are zero?
(c) At how many point f'(x) is negative ?
(d) Which is the point of inflection?

View SolutionGraph of functions are given in the following figure. Check the functions for absolute extremum.
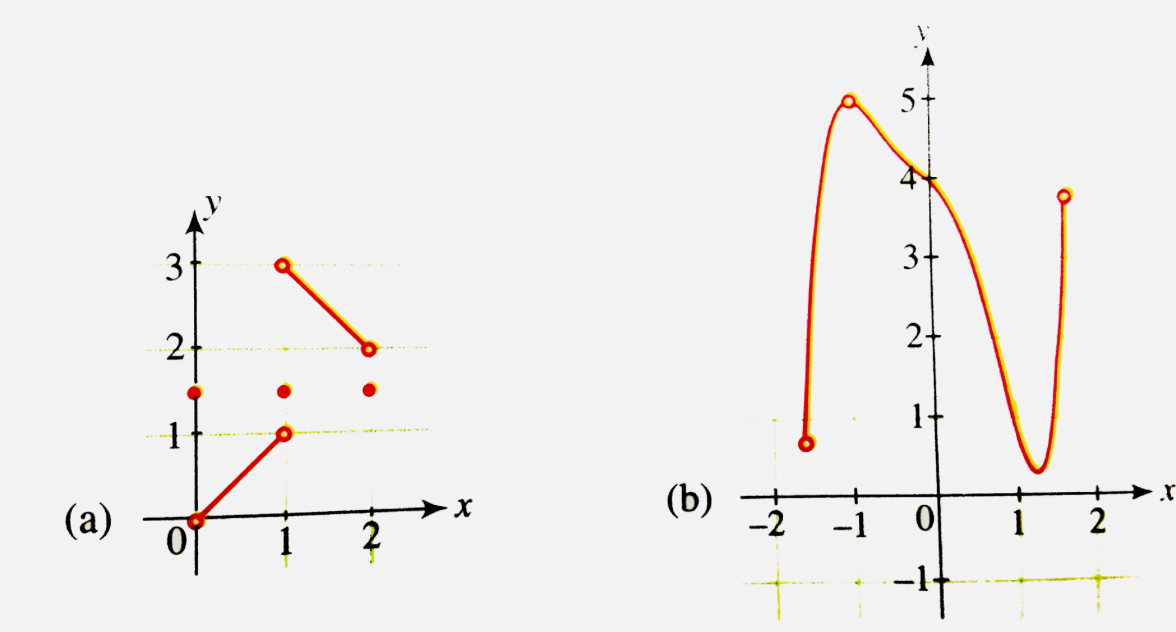
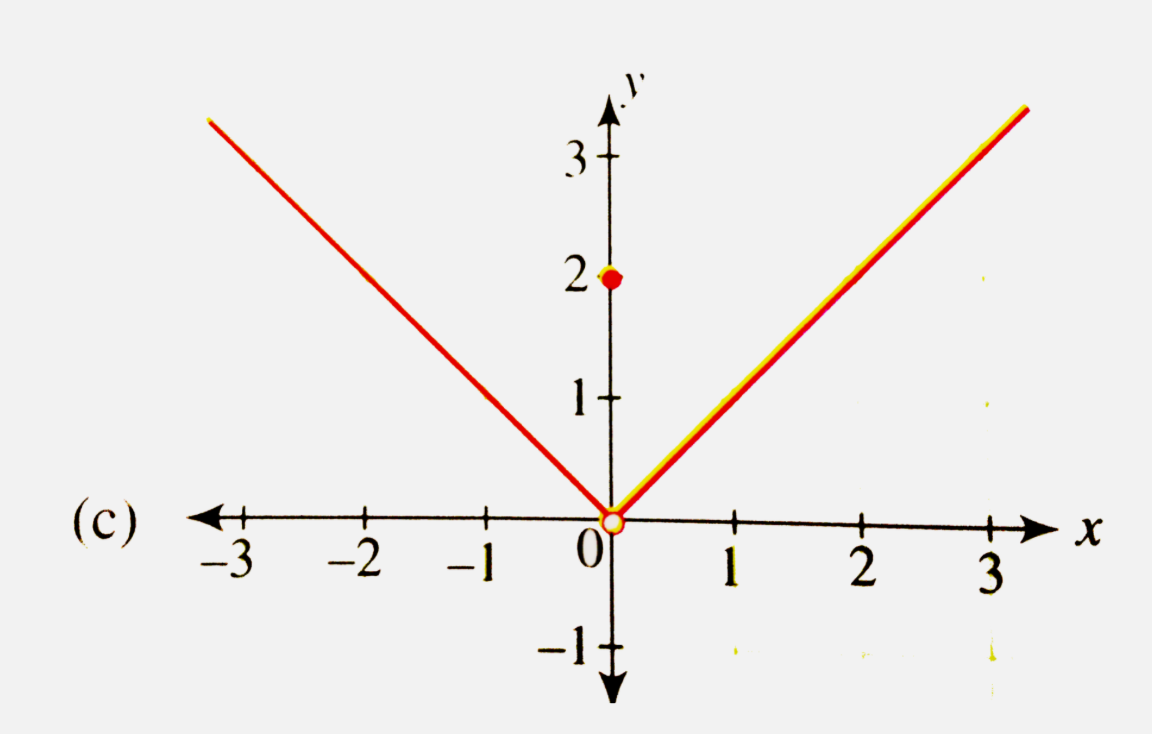
View SolutionSelect the right option regarding the given graph.
View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionThe graph of f is given.
State the equations of all the asymptotes.

View Solution(a) Can the graph of the function intersect the horizontal asymptote?
(b) Can the graph of the function intersect the vertical asymptote?
View SolutionWrite a possible rational function h with a hole at x = 5, a vertical asymptote at x = -1, a horizontal asymptote at y = 2 and x-intercept at x = 2.
View SolutionWrite a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.
View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
View SolutionThe asymptotes of a rectangular hyperbola intersect at an angle
View SolutionThe point of intersection of the asymptotes with the directrices lie on
View Solution(a) Can the graph of the function intersect the horizontal asymptote?
(b) Can the graph of the function intersect the vertical asymptote?
View SolutionWrite a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.
View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
View Solution
