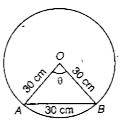
A chord of a circle of diameter 30 cm is of length 15 cm. Find the length of mirror arc corresponding to this chord.
Here, AB=15 cm
OA=OB= radius of circle = 15 cm
Therefore, ΔAOB, is an equilateral triangle.
⇒∠AOB=60∘
=(60xπ180) radian
=227×3 radian =2221 radian
∴ Length of minor arc = radius of circle × angle subtended by this arc at the center
=15×2221cm=1107cm=15(57)cm.
Topper's Solved these Questions
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3A
12 Videos
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3B
24 Videos
- STRAIGHT LINESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise
207 Videos
Similar Questions
In a circle of diameter 40 cm. The length of a chord is 20 cm. Find the length of minor arc of the chord.
View SolutionIn a circle of diameter 60 cm the length of a chord is 30 cm. Find the length of the minor and major arcs of the chord.
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of sector of the circle formed by chord AB .
View SolutionA chord of a circle of radius 15 cm subtends an angle of 60∘at the centre. Find the areas of the corresponding minor and major segments of the circle.
View SolutionArea of a sector of central angle 200∘ of a circle is 770cm2 . Find the length of the corresponding arc of this sector.
View SolutionTwo concentric circles are of diameters 30cm and 18cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionThe radius of a circle is 15cm. Find the length of its longest chord.
View SolutionA chord of a circle of radius 12 cm subtends an angle of 120∘at the centre. Find the area of the corresponding segment of the circle.
View SolutionThe height of circular arc ACB is 0.6 m. if the radius of circle is 3m , then find the length of the corresponding chord.

View SolutionA chord of a circle of radius 10cm subtends a right angle at the centre. The length of the chord (in cm) is
View Solution
