A circle C whose radius is 1 unit touches the x-axis at point A. The center Q of C lies in the first quadrant. The tangent from the origin O to the circle touches it at T and a point P lies on its such that ΔOAP is a right - angles triangle at A and its perimeter is 8 units.
The length of PQ is
3y=4x
x−√2y=0
y−√3x=0
none of these
The correct Answer is:1
AP=AQ+PQ=1+5/3=8/3
So, slope of OP is 4/3
Hence, equation of OP is 4x−3y=0.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE21videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - ARCHIVES (JEE MAIN)1videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
A circle C whose radius is 1 unit, touches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circie touches it at T and a point P lies on it such that ΔOAP is a right angled triangle at A and its perimeter is 8 units. The length of QP is
View SolutionA circle of radius 6 units touches the coordinates axes in the first quadrant. Find the equation of its image in the line mirror y=0.
View SolutionA circle touches the y-axis at the point (0, 4) and cuts the x-axis in a chord of length 6 units. Then find the radius of the circle.
View SolutionA circle touches the y-axis at the point (0, 4) and cuts the x-axis in a chord of length 6 units. Then find the radius of the circle.
View SolutionA circle touches both the x-axis and the line 4x−3y+4=0. Its centre is in the third quadrant and lies on the line x−y−1=0. Find the equation of the circle.
View SolutionA circle having its centre in the first quadrant touches the y-axis at the point (0,2) and passes through the point (1,0). Find the equation of the circle
View SolutionCircles are drawn through the point (2, 0) to cut intercept of length 5 units on the x-axis. If their centers lie in the first quadrant, then find their equation.
View SolutionThe distance of the y - axis from from the center of the circle which lies in the first quadrant (see figure) and tangent to the lines y=12x,y=4 and the x-axis is
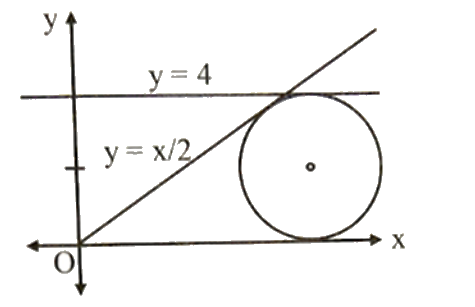 View Solution
View SolutionThe circle C has radius 1 and touches the line L at P. The point X lies on C and Y is the foot of the perpendicular from X to L. The maximum value of the area of △PXY as X varies is
View SolutionA circle of radius 2 units touches the co ordinate axes in the first quadrant. If the circle makes a complete rotation on the x-axis along the positive direction of the x-axis, then the equation of the circle in the new position is
View Solution

