Question

A circle has radius $\sqrt{2}$cm it is divided into 2 segments by a chord of length 2cm prove that angle subtended by the chord at a point in major segment is ${45}^{\circ }$

Explanation

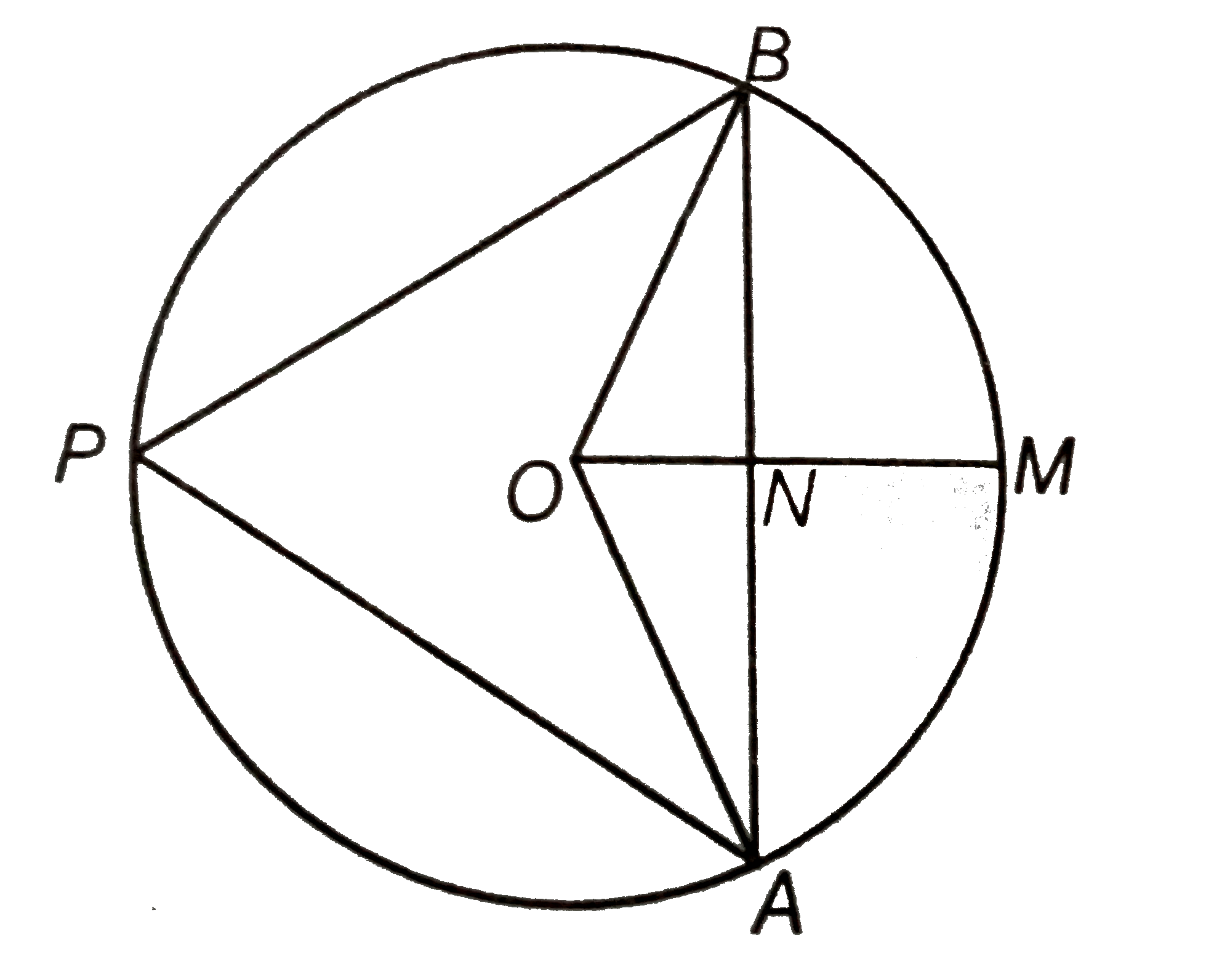
Draw a circle having centre O. Let AB=2 cm be a chord of a circle. A chord AB is divided by the line OM in two equal segments.
To prove ` angleAPB=45^(@)`
Here, AN=NB = 1 cm
and ` OB=sqrt2 c m `
In `DeltaONB, OB^(2)=ON^(2)+NB^(2)`
[use Pythagoras theorem]
`rArr (sqrt2)^(2)=ON^(2)+(1)^(2)`
` rArr ON^(2)=2-1=1`
`rArr ON=1 cm`
[taking positive square root, because distance is always positive]
Also, `angleONB=90^(@)` [ON is the perpendicular bisector of the chord AB]
`:. angleNOB=angleNBO=45^(@)`
Similarly, `angleAON=45^(@)`
Now, ` angleAOB=angleAON+angleNOB`
`=45^(@)+45^(@)=90^(@)`
We know that, chord subtends an angle to the circle is half the angle subtended by it to the centre.
`:. angleAPB=1/2 angleAOB`
` =90^(@)/2=45^(@)`