A circle of radius 1 unit touches the positive x-axis and the positive y-axis at AandB , respectively. A variable line passing through the origin intersects the circle at two points DandE . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
The equation of the circle is
(x−1)2+(y−1)2=1
or x2+y2−2x−2y+1=0 (1)
Let the equation of the variable straight line through origin be
y=mx (2)
This line intersects the cricle at two points D and E.
Distance of line from point B(0,1) is
BM=|m(0)−1|√1+m2=1√1+m2
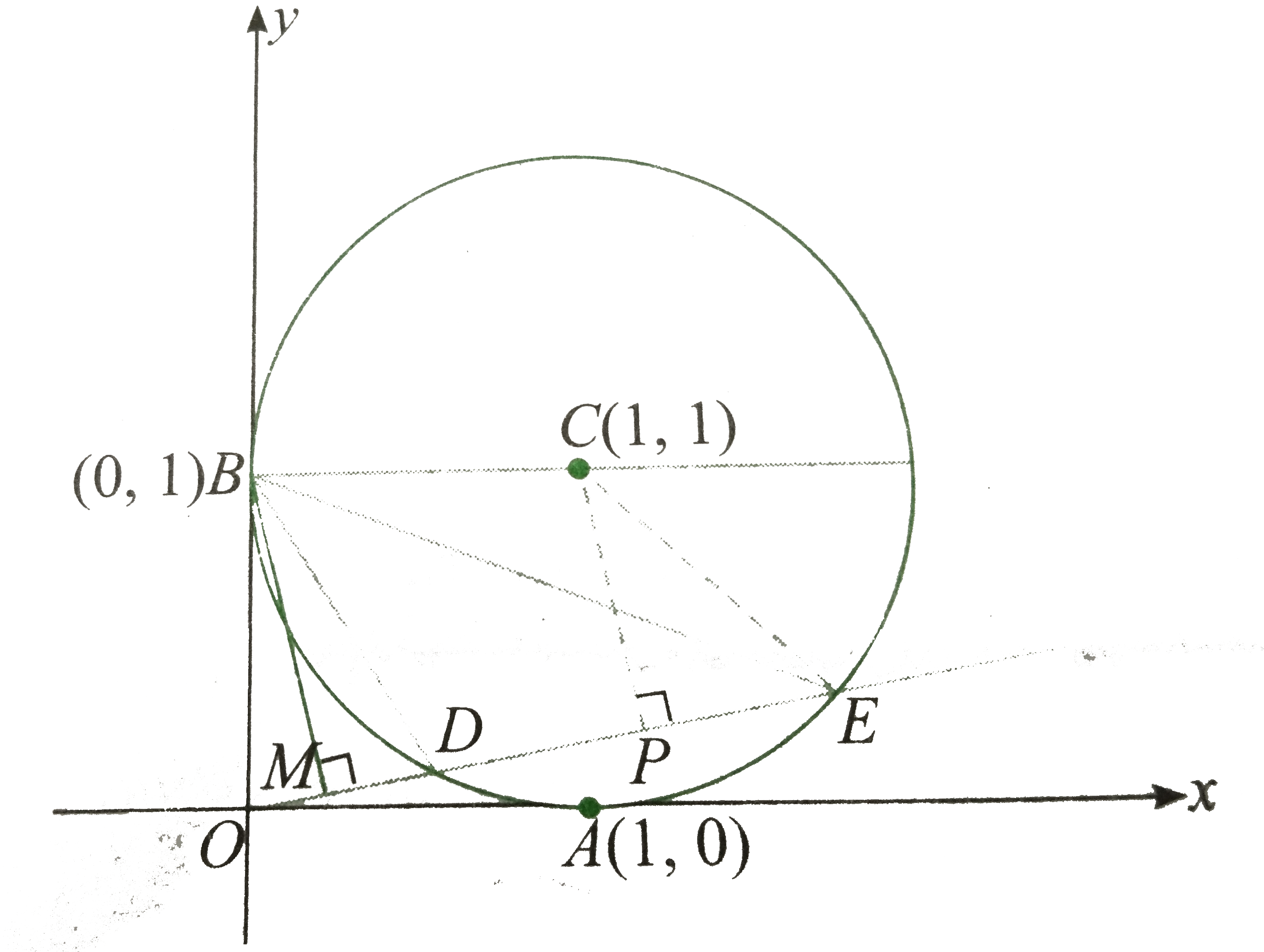
Also, CP=|m(1)−1|√1+m2=|m−1|√1+m2
∴DE=2PE=2√CE2−CP2=2√1−(m−1)21+m2=2√2m1+m2
∴Area of triangle DEB.
Δ=12BM×DE
=121√1+m2×2√2m1+m2=√2m1+m2
Differentiating Δ w.r.t. m, we get
dΔdm=√2⎡⎢⎣12√m(1+m2)−2m√m(1+m2)2⎤⎥⎦=1−3m2√2√m(1+m2)2
If dΔdm=0 , then m=1√m, whichi is point of maxima.
Therefore, area is maximum if m=1√3.
Topper's Solved these Questions
Similar Questions
A circle of radius 1 unit touches the positive x-axis and the positive y-axis at AandB , respectively. A variable line passing through the origin intersects the circle at two points DandE . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View SolutionIf a line passing through the origin touches the circle (x−4)2+(y+5)2=25 , then find its slope.
View Solution
Knowledge Check
A line L passing through the focus of the parabola y2=4(x−1), intersects the parabola in two distinct points. If 'm' be the slope of the line 'L' then
A-1 lt m lt 1B,<−1 or m>1Cm in RDNone of the aboveA line L passing through the focus of the parabola y2=4(x−1), intersects the parabola in two distinct points. If 'm' be the slope of the line 'L' then
A−1<m<1Bm<−1orm>1Cm∈RDnone of theseA line L passing through the focus of the parabola (y−2)2=4(x+1) intersects the two distinct point. If m be the slope of the line I,, then
Amin(−∞,−1)∪(1,∞)Bm∈(−∞,0)∪(0,∞)Cmin(−∞,0)∪(0,∞)Dnone of these
P is a point on positive x-axis, Q is a point on the positive y-axis and 'O' is the origin. If the line passing through P and Q is tangent to the curve y=3−x2 then find the minimum area of the triangle OPQ , is 3 (b) 4 (c) 5 (c) 6
View SolutionCircle with centre C (1, 1) passes through the origin and intersects the x-axis at A and y-axis at B. The area of the part of the circle that lies in the first quadrant is
View SolutionIf the radisu of the circle passing through the origin and touching the line x+y=2 at (1,1) is r units, then the value of 3√2r is
View SolutionA circle C is tangent to the x and y axis in the first quadrant at the points P and Q respectively. BC and AD are parallel tangents to the circle with slope –1. If the points A and B are on the y-axis while C and D are on the x-axis and the area of the figure ABCD is 900 . √2 sq. units then find the radius of the circle.
View SolutionA circle passes through the points of intersection of the parabola y+1=(x–4)2 and x-axis. Then the length of tangent from origin to the circle is
View Solution
