A corner point of a feasible region is a point in the reqion which is the of two boundary lines.
The correct Answer is:N/a
A corner point of a feasible region is a point in the region which is the intersection of boundary lines
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - TRUE/FALSE
2 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - OBJECTIVE
8 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
In a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
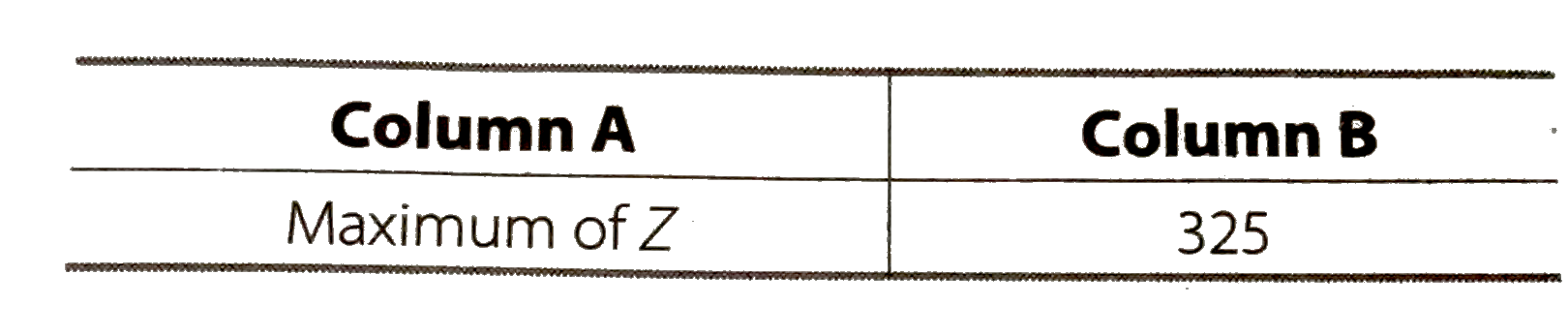
View Solution
Knowledge Check
In an L.P.P. if the objective function Z=ax+by by has same maximum value on two corner points of the feasible region, then the number of points at which maximum value of Z occurs is
A0B2CfiniteDinfiniteThe corner points of the feasible region determine by the system of linear constrainsts are (0,10) ,(5,5) ,(15,15),(0,20),Let Z=px +qy , where p,q>0. Conditions on p and q so that the maximum of Z occurs at the point (15,15) and (0,20) is
Ap=qBp=2qCq=2pDq=3pA line containing point (2,4) has slope 3. If point P lies on this line , which of the following could be point P ?
A(3,7)B(2,6)C(2,7)D(3,-1)
For LPP problems the feasible region always falls on which quadrant?
View SolutionSketch the regions which points satisfy |x+y|≥2.
View SolutionPlot the points A(1,-1) and B(4,5).
(i) Draw the line segment joining these points. Write the coordinates of a point on this line segment between the points A and B.
(ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.
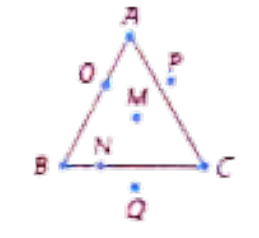
View SolutionIn the figure given below. Find .
(a) the points that lie in the interior of the given figure.
(b) The points that lie on the boundary of the triangles.
(c ) the points that lie on the exterior of the triangle.
View SolutionTwo equal point charges Q=+√2μC are placed at each of the two opposite corners of a square and equal point charges q at each of the other two corners. What must be the value of q so that the resultant force on Q is zero?
View Solution
