Two equal point charges Q=+√2μC are placed at each of the two opposite corners of a square and equal point charges q at each of the other two corners. What must be the value of q so that the resultant force on Q is zero?
The correct Answer is:−12μC
To solve the problem, we need to determine the value of charge q such that the resultant force on charge Q is zero. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Configuration
We have a square with two equal charges Q=+√2μC placed at two opposite corners. The other two corners have equal charges q. We need to find q such that the net force on Q is zero.
Step 2: Identify Forces Acting on Charge Q
The forces acting on charge Q are:
- The attractive forces due to the charges q at the other two corners.
- The repulsive forces due to the other charge Q.
Step 3: Calculate the Distance Between Charges
Let the side length of the square be a. The distance between the charges Q and q is a, and the distance between the two charges Q is a√2 (the diagonal of the square).
Step 4: Write the Expression for Forces
The force between charge Q and charge q is given by Coulomb's law:
FQq=14πϵ0⋅Q⋅qa2
The force between the two charges Q is:
FQQ=14πϵ0⋅Q2(a√2)2=14πϵ0⋅Q22a2
Step 5: Set Up the Force Balance
Since the forces due to the two charges q must balance the repulsive force from the other charge Q, we can express this as:
2FQq=FQQ
Substituting the expressions for the forces:
2(14πϵ0⋅Q⋅qa2)=14πϵ0⋅Q22a2
Step 6: Simplify the Equation
Cancel 14πϵ0 and a2 from both sides:
2Qq=Q22
Step 7: Solve for q
Rearranging gives:
q=Q4
Step 8: Substitute the Value of Q
Substituting Q=√2μC:
q=√2μC4=√24μC
Step 9: Calculate the Final Value of q
To express q in a more standard form:
q=√24μC=12√2μC≈0.3535μC
Final Answer
Thus, the value of q that makes the resultant force on Q zero is:
q=0.3535μC
We have a square with two equal charges Q=+√2μC placed at two opposite corners. The other two corners have equal charges q. We need to find q such that the net force on Q is zero.
The forces acting on charge Q are:
- The attractive forces due to the charges q at the other two corners.
- The repulsive forces due to the other charge Q.
Let the side length of the square be a. The distance between the charges Q and q is a, and the distance between the two charges Q is a√2 (the diagonal of the square).
The force between charge Q and charge q is given by Coulomb's law:
FQq=14πϵ0⋅Q⋅qa2
The force between the two charges Q is:
FQQ=14πϵ0⋅Q2(a√2)2=14πϵ0⋅Q22a2
Since the forces due to the two charges q must balance the repulsive force from the other charge Q, we can express this as:
2FQq=FQQ
Substituting the expressions for the forces:
2(14πϵ0⋅Q⋅qa2)=14πϵ0⋅Q22a2
Cancel 14πϵ0 and a2 from both sides:
2Qq=Q22
Rearranging gives:
q=Q4
Substituting Q=√2μC:
q=√2μC4=√24μC
To express q in a more standard form:
q=√24μC=12√2μC≈0.3535μC
Thus, the value of q that makes the resultant force on Q zero is:
q=0.3535μC
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[B]
16 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(A)
35 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 9
2 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
A charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
View SolutionA charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
View SolutionA charge Q is place at each of the opposite corners of a square. A charge q is placed at each of the other two corners. If the net electrical force on Q is zero, then Q/q equals:
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
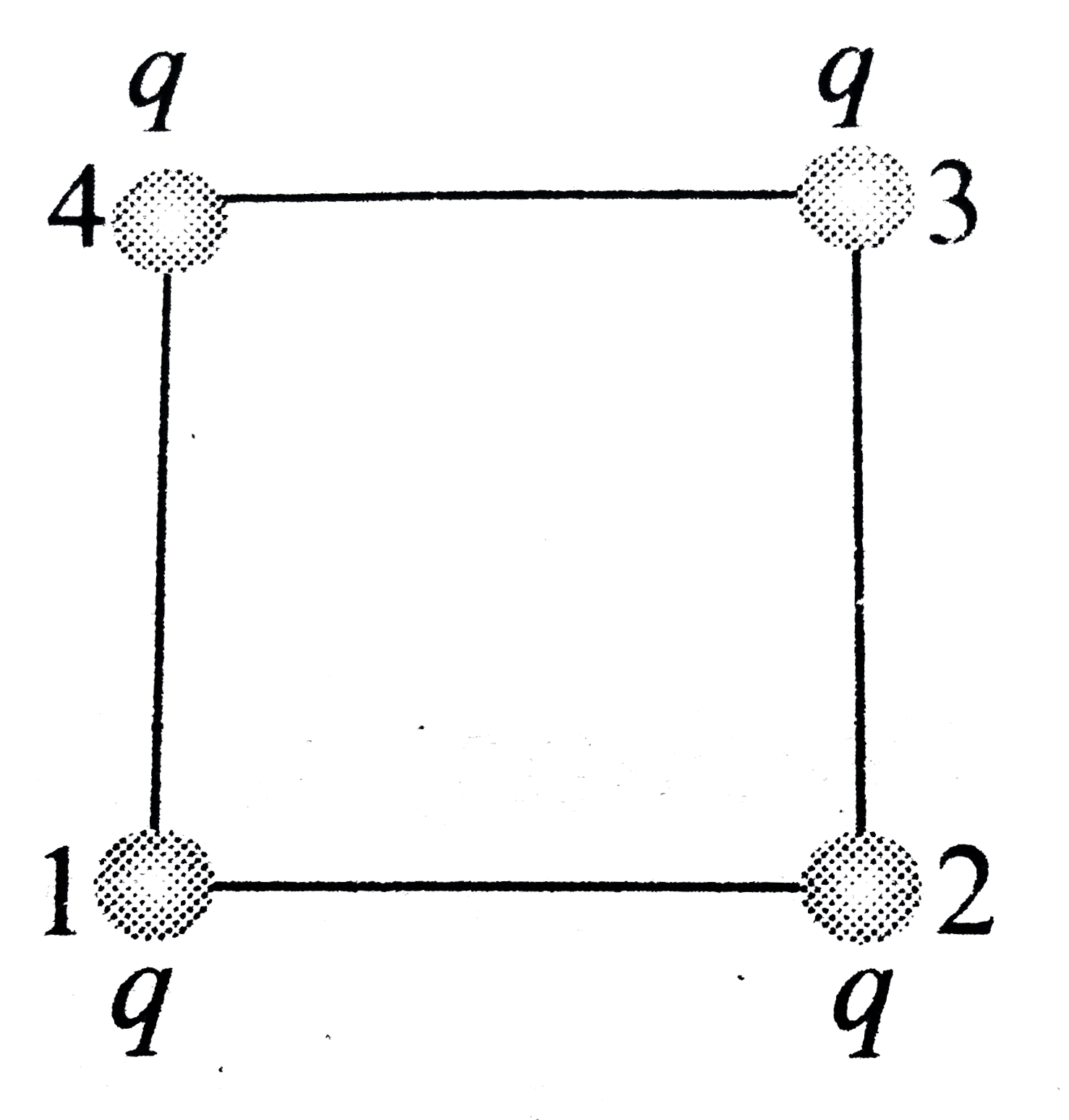 .
.
View SolutionFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
View SolutionSix equal point charges q each are placed at six corners of a hexago of side a. Find out potential energy of charge system
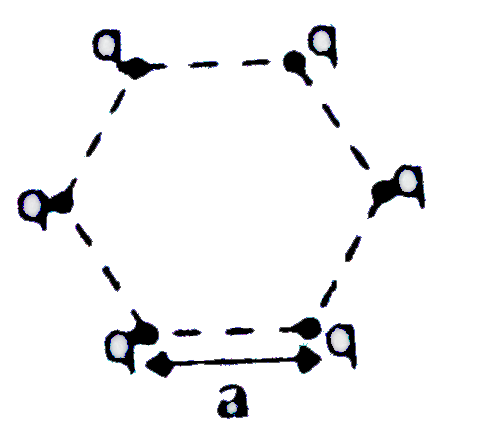
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View SolutionFour positive charges (2√2−1)Q are arranged at the four corners of a square. Another charge q is placed at the centre of the square. Resulting force acting on each corner charge is zero if q is
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View Solution
