A discret random variable `X` has the following probability distribution: `X :1234567` `P(X):c2c2c3cc^22c^27c^2+c` Find the value of `cdot` Also, find the mean of the distribution.
To solve the problem step by step, we will first find the value of c in the given probability distribution and then calculate the mean of the distribution.
Step 1: Set Up the Probability Distribution Equation
The given probability distribution is:
- P(X=1)=c
- P(X=2)=2c
- P(X=3)=2c
- P(X=4)=3c
- P(X=5)=c2
- P(X=6)=2c2
- P(X=7)=7c2+c
Since the sum of all probabilities must equal 1, we can write:
c+2c+2c+3c+c2+2c2+(7c2+c)=1
Step 2: Combine Like Terms
Combining the terms, we have:
c+2c+2c+3c+c+2c2+7c2=1
This simplifies to:
9c+10c2=1
Step 3: Rearrange the Equation
Rearranging gives us a quadratic equation:
10c2+9c−1=0
Step 4: Solve the Quadratic Equation
To solve the quadratic equation 10c2+9c−1=0, we can use the quadratic formula:
c=−b±√b2−4ac2a
where a=10,b=9,c=−1.
Calculating the discriminant:
b2−4ac=92−4⋅10⋅(−1)=81+40=121
Now substituting into the formula:
c=−9±√1212⋅10=−9±1120
Calculating the two possible values:
1. c=220=110
2. c=−2020=−1
Since probabilities cannot be negative, we take:
c=110
Step 5: Calculate the Mean of the Distribution
The mean μ of the distribution is given by:
μ=7∑i=1xiP(X=xi)
Substituting the values:
μ=1⋅c+2⋅2c+3⋅2c+4⋅3c+5⋅c2+6⋅2c2+7⋅(7c2+c)
Substituting c=110:
μ=1⋅110+2⋅2⋅110+3⋅2⋅110+4⋅3⋅110+5⋅(110)2+6⋅2⋅(110)2+7⋅(7⋅(110)2+110)
Calculating each term:
- 1⋅110=110
- 2⋅2⋅110=410
- 3⋅2⋅110=610
- 4⋅3⋅110=1210
- 5⋅(110)2=5100=0.0510
- 6⋅2⋅(110)2=12100=0.1210
- 7⋅(7⋅(110)2+110)=7⋅(7100+10100)=7⋅17100=119100=1.1910
Adding these together:
μ=1+4+6+12+0.05+0.12+1.1910=24.3610=2.436
Final Answers
- The value of c is 110.
- The mean of the distribution is 2.436.
The given probability distribution is:
- P(X=1)=c
- P(X=2)=2c
- P(X=3)=2c
- P(X=4)=3c
- P(X=5)=c2
- P(X=6)=2c2
- P(X=7)=7c2+c
c+2c+2c+3c+c2+2c2+(7c2+c)=1
Combining the terms, we have:
c+2c+2c+3c+c+2c2+7c2=1
This simplifies to:
9c+10c2=1
Rearranging gives us a quadratic equation:
10c2+9c−1=0
To solve the quadratic equation 10c2+9c−1=0, we can use the quadratic formula:
c=−b±√b2−4ac2a
where a=10,b=9,c=−1.
b2−4ac=92−4⋅10⋅(−1)=81+40=121
c=−9±√1212⋅10=−9±1120
1. c=220=110
2. c=−2020=−1
c=110
The mean μ of the distribution is given by:
μ=7∑i=1xiP(X=xi)
μ=1⋅c+2⋅2c+3⋅2c+4⋅3c+5⋅c2+6⋅2c2+7⋅(7c2+c)
μ=1⋅110+2⋅2⋅110+3⋅2⋅110+4⋅3⋅110+5⋅(110)2+6⋅2⋅(110)2+7⋅(7⋅(110)2+110)
- 1⋅110=110
- 2⋅2⋅110=410
- 3⋅2⋅110=610
- 4⋅3⋅110=1210
- 5⋅(110)2=5100=0.0510
- 6⋅2⋅(110)2=12100=0.1210
- 7⋅(7⋅(110)2+110)=7⋅(7100+10100)=7⋅17100=119100=1.1910
μ=1+4+6+12+0.05+0.12+1.1910=24.3610=2.436
- The value of c is 110.
- The mean of the distribution is 2.436.
Topper's Solved these Questions
Similar Questions
A random variable X has the following distribution

View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View SolutionA random variable X has the following probability distribution :

determine the value of a
View SolutionA discrete random variable X has the probability distribution given below: X:0.511.52 P(X):kk22k2k Find the value of k. (ii) Determine the mean of the distribution.
View SolutionA random varibale X has the following probability distribution.
X:12345P(X):00.10.20.30.4
Find the mean.
View SolutionIf X is a random variable with the following probability distribution
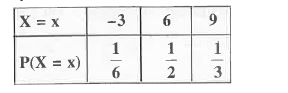
then the variance of X is
View SolutionA random variable X has the following distribution
x:1234P(X=x):k23k25k27k2
The value of k is
View SolutionA random variable X has the following distribution
x1234P(X=x)c2c3c4c
The value of c is
View SolutionA random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View SolutionA random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View Solution
