A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftmans time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P. and solve graphically.
Let x= number of tennis rackets and y= number of cricket bats produced in one day in the factory.
Therefore
Maximize profit z=20x+10y
Subject to: x≥0
y≥0
1.5x+3y≤42
⇒x+2y≤28
and 3x+y≤24
Draw the graph of the equations x=0,y=0,x+2y=28 and 3x+y=24
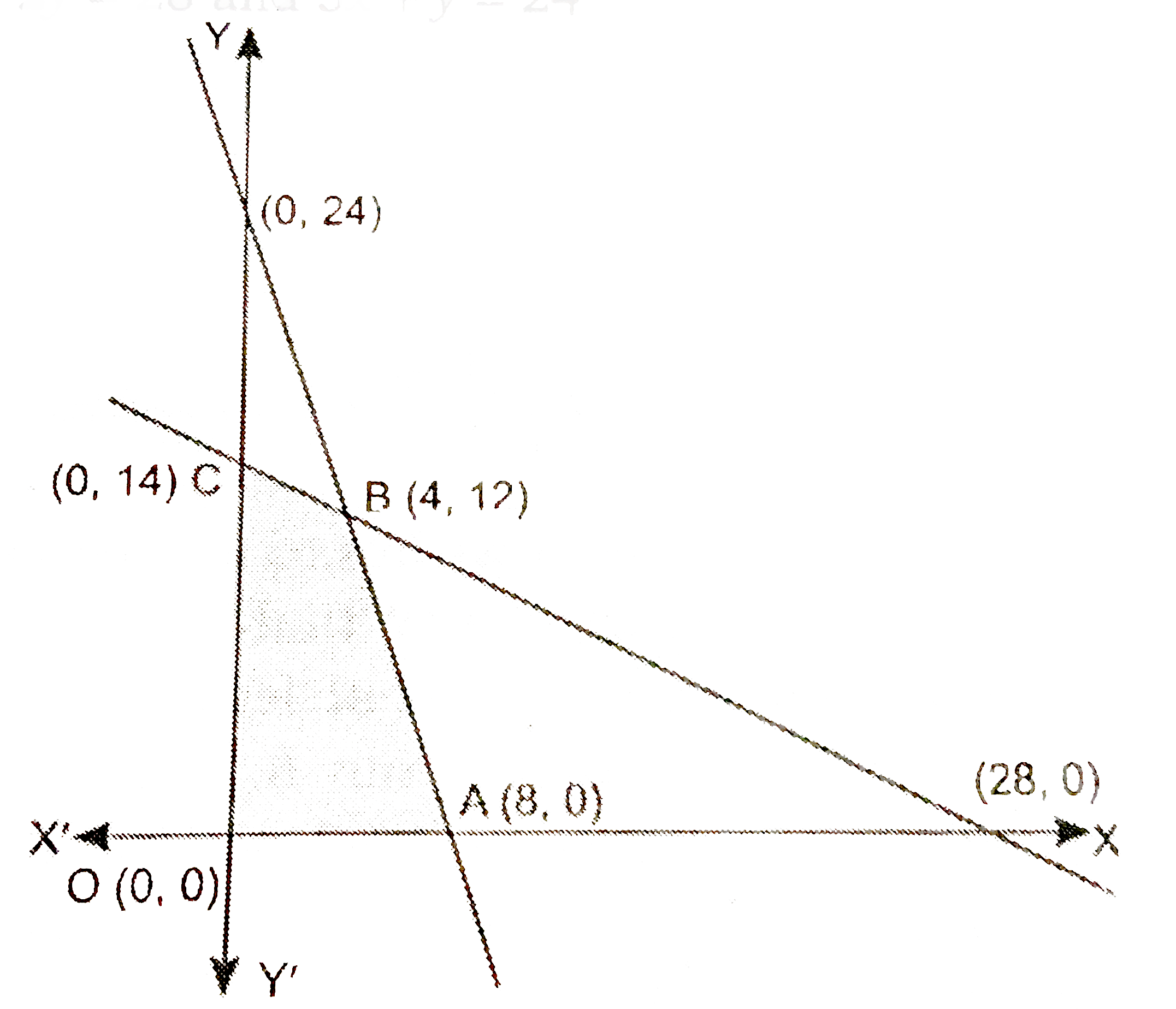
Now obtain the feasible region for the inequations x≥0,y≥0,x+2y≤28 and 3x+y≤24 and shade it. The convex region is OABC whose vertices are A(8,0),B(4,12),C(0,14) an O(0,0). We will find the value of z at these vertices.

The maximum profit is Rs. 200 which can be obtained if 4 tennis rackets and 12 cricket bats produced in one day.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 A
8 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 B
17 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftmans time m its making while a cricket bat takes 3 hour of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time.(i) What number of rackets and bats must be made if the factory is to work at full capacity?(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.
View SolutionA factory makes tennis rackets and cricket bats. A tennis rackets takes 1.5 hour of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hour of machine time and 1 hour of cratman's time. In a daythe factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time.
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the maximum profit of the factory when it works at full capacity.
View Solution
Knowledge Check
A firm makes pants and shirts . A shirt takes 2 hours on machine and 3 hours of man lobour while a pant takes 3 hours on machine and 2 hours of man labour .In a week , there are 70 hours of machine and 75 hous of man lobour available . If the firm dertermines to make x shirts and y pants per week , then for this linear constraints are
Ax≥0,y≥0,2x+3y≥70,3x+2y≥75Bx≥0,y≥0,2x+3y≤70,3x+2y≥75Cx≥0,y≥0,2x+3y≥70,3x+2y≤75Dx≥0,y≥0,2x+3y≤70,3x+2y≤75A tailor stiches trousers and shirts and each piece is completed by two machine I and II. To complete each trousers, machines I and II must work 3/2 hours and 2 hours respectively, and to complete each shirt, machines I and II must work 2 hours and 1 hours respectively Machine I may not operate for more than 12 hours ped day and machine II not more than 11 hours per day. If the profit on each trouser and each shirt is Rs. 150 and Rs. 100 repectively, then the maximum profit is _______
ARs. 900BRs. 500CRs. 375DRs. 600
A factory makes cricket bats and tennis rackets. A cricket bat takes 1.5 hours of machine time and 2 hours of craftsman's time, while a tennis racket takes 2.5 hours of machine time and 1.5 hours of craftsman's time. In aday the factory has available upto 80 hours of machine time and 70 hours of craftsman's time.
What is the largest number of (i) bats, (ii) rackets which could be made in a day in the factory ?
View SolutionA factory makes cricket bats and tennis rackets. A cricket bat takes 1.5 hours of machine time and 2 hours of craftsman's time, while a tennis racket takes 2.5 hours of machine time and 1.5 hours of craftsman's time. In aday the factory has available upto 80 hours of machine time and 70 hours of craftsman's time.
What number of bats and rackets must be made if the factory is to work at full capacity ?
View SolutionA factory makes cricket bats and tennis rackets. A cricket bat takes 1.5 hours of machine time and 2 hours of craftsman's time, while a tennis racket takes 2.5 hours of machine time and 1.5 hours of craftsman's time. In aday the factory has available upto 80 hours of machine time and 70 hours of craftsman's time.
The profit on a bat and on a racket is Rs. 5 and Rs. 3.50 respectively. Find the maximum profit to the factory on a day when it produces (i) only bats, (ii) only rackets and (iii) works at full capacity.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades.Both the products require machine time as well as craftsman time in the making.The number of hours required for producing 1 unit of each and the corresponding profit is given in the following table:
In a day,the factory has availability of not more than 42 hours of machine time and 24 hours of craftsman time.
Assuming that all items manufactured are sold,how should the manufacturer schedule his daily production in order to maximise the profit?Formulate it as an LPP and solve it graphically
View SolutionA company manufactures bicycles and tricycles, each of which must be processed through two machines A and B. Machine A has maximum of 120 hours available and machine B has a maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are ₹ 180 for a bicycle and ₹ 220 for a tricycle, determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
View SolutionA company manufacture is bicyles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours avaiable and machine B has maximum of 180 hours available hours on machine A and 3 hours on machine B. Machine A and 10 hours on machine B.
If profit are ₹ 180 for a bicyle and ₹ 220 for a tricyle , formulate and solve the L.P.P to determine the number of bicycles and tricycle that should be manufactured in order to maximize the profit .
View Solution
