A factory owner purchase two types of machines A and B for his factory. The requirements and the limitations for the machines are as follows :

He has maximum area of 9000m2 available and 72 skilled laborer's who can operate both the machines. How many machines of each type should he buy to maximize the daily output ?
Let x machines of type A and y machines of type B be boutht and let z be the daily putput.
Then,z=60x+40y. ...(i)
maxium area available =9000m2.
∴1000x+1200y≤9000
⇒5x+6y≤45. ...(ii)
Maximum labour available =72 men.
∴12x+8y≤72⇒3x+2y≤18. ...(iii)
Now, we have to maximize z=60x+40y, subject to the constraints
5x+6y≤45,
3x+2y≤18,
x≥0andy≥0.
Now, 5x+6y=45⇒x9+y(15/2)=1.
This line meets the axes at A(9,0)andB(0,152).
Plot these points and join them to obtin the line 5x+6y=45.
Clearly, (0,0) satisfies 5x+6y≤45.
So, the regon below AB represents 5x+6y≤45.
Again, 3x+2y=18⇒x6+y9=1.
This line meets the axes at C(6,0)andD(0,9).
Plot these points and join them to obtain the line 3x+2y=18.
Clearly, (0,0) satisfies 3x+2y≤18.
So, the region below CD represents 3x+2y≤18.
x≥0 is the region above the x-axis
And, y≥0 is the region above the x-axis.
On solving 5x+6y=45and3+3x+2y=18 simultaneously, we get x=94andy=458.

So, the line AB and CD intersect at F(94,458).
Thus, the corner points of the feasible regin are O(0,0),C(6,0),E(94,458)andB(0,152).
Value of daily output z=60x+40y:
(i) At O(0,0)itisz=(60×0+40×0)=0.
(ii) At C(6,0)it is z=(60×6+40×0)=360.
(iii) At E(94,152)it isz=(60×94+40×458)=360.
(iv) At B(0,152)it is z=(60×0+40×152)=300.
Thus either (6 machines of type A and no machine of type B) or (2 machines of type A and 6 machines of type B) be used to have maximum uutput.
[Note 94 machines =−2 machines and 458 machines =−6 machines.]
Similar Questions
A factory owner purchases two types of machines, A and B for his factory. The requirements and the limitations for the machines are as follows: Machine Area occupied Labour force Daily output (in units) A 1000 m2 12 men 60 B 1200 m2 8 men 40 He has maximum area of 9000 m2 available, and 72 skilled labourers who can operate both the machines. How many machines of each type should he buy to maximise the daily output?
View SolutionA factory owner purchases two types of machines, A and B for his factory. The requirements and the limitations for the machines are as follows: Machine Area occupied Labour force Daily output (in units) A 1000 m2 12 men 60 B 1200 m2 8 men 40 He has maximum area of 9000 m2 available, and 72 skilled labourers who can operate both the machines. How many machines of each type should he buy to maximise the daily output?
View Solution
Knowledge Check
A factory owner wants to purchase 2types of machines A ,and B for his factory . The machine A requires an area of 1000m2 and 12 skilled men for running it ans its daily output is 50 units , whereas the machine B rquires 1200m2 area and 8 skilled men and its daily output is 40 units .If an area of 7600m2and72 skilled men are available to operate the machines . The linear constraints are
A1000x+1200y≤7600,12x+8y≤72,x≥0,y≥0B1000x+1200y≥7600,12x+8y≤72,x≥0,y≥0C1000x+1200y≤7600,12x+8y≥72,x≥0,y≥0D1000x+1200y≥7600,12x+8y≥72,x≥0,y≥0
A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package on screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacturer a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs. 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day order to maximise his profit? Determine the maximum profit.
View SolutionA factory manufatures two types pf screws A and B, Each type of screw requires the use of two machines, an automatic and a hand operated.It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B.Each machine is available for at the most 4 hours on any day.The manufacturer can sell a package of screws A at a profit of ₹ 7 and screws B at a profit of ₹ 10.Assuming that he can sell all the screws he amnufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit?Determine the maximum profit.
View SolutionA manufacturer has three machines A,B and C installed in his factory. Machines A and B are capable of being operated for atmost 12 hours whereas machine C must be operated for atleast 5 hours a day. He produces only two items X and Y each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of X and Y on three machines are given in the following table:
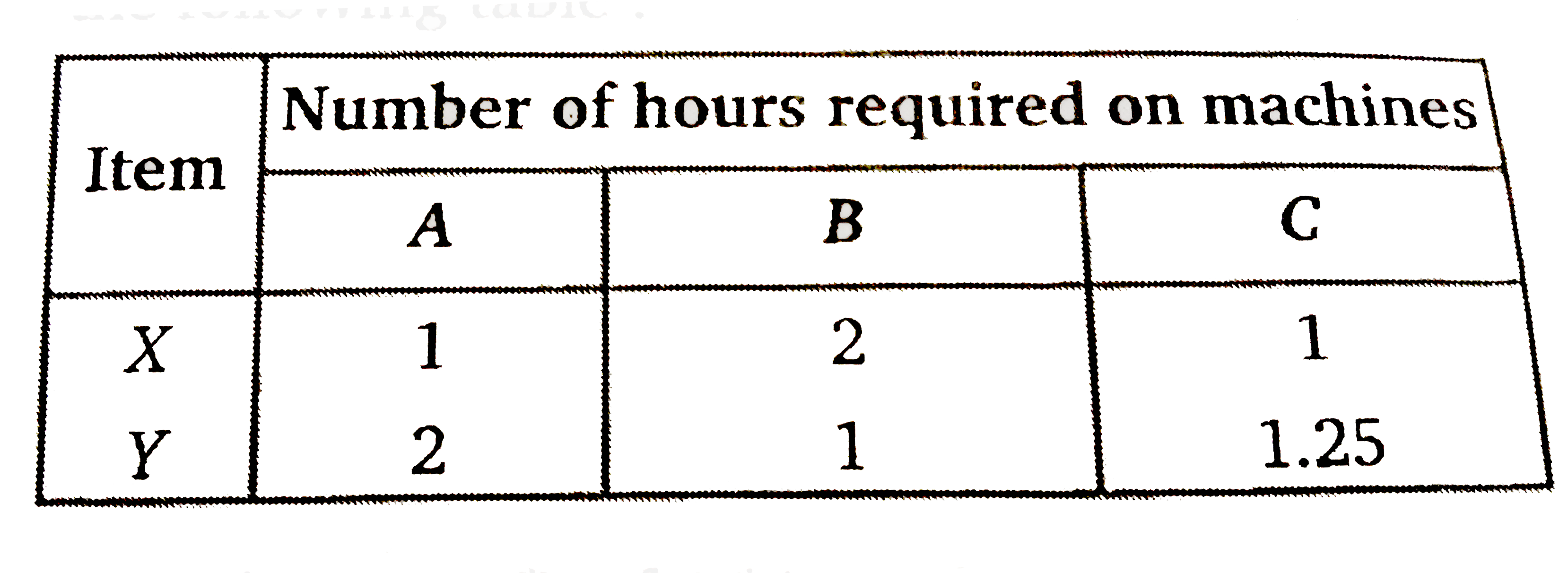
He makes a profit of Rs. 600 and Rs. 400 on each item of X and Y respectively. How many of each item should he produce so as to maximize his profit assuming that he can sell all the items that he produced?
View SolutionIn a small scale industry, a manufacturer produces two types of book cases. The first type of book case requires 3 hours on machine A and 2 hours on machine B for completion whereas the second type of book case requires 3 hours on machine A and 3 hours on machine B. The machines A and B respectively run for at the most 18 hours and 14 hours per day. He earns a profit of 30 on each type of case of first type and 40 on each book case of second type. How many book cases of each type should he manufacture so as to have maximum profit. Make it an LPP and solve it graphically.
View Solution(Manufacturing problem) A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine HI must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of M and N on the three machines are given m the following table:She makes a profit of Rs 600 and Rs 400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
View SolutionA manufacture makes two types of cups A and B. Three machines are required to manufacture the cups and the time in minutes required by each in as given below:

Each machine is available for a maximum period of 6 hours per day. If the profit on each cup A is 75 paisa and on B is 50 paisa, find how many cups of each type should be manufactures to maximise the profit per day.
View Solution
