A farmer mixes two brands $P$ and $Q$ of cattle feed. Brand $P$ costing Rs. 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand $Q$ costing Rs. 200 per bag contains 1.5 units of nutritonal element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A,B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?

Video Solution

Text Solution

Verified by Experts

Let the farmer mixed $x$ bags of type $P$ and $y$ bags of type $Q$ cattle feeds. Then

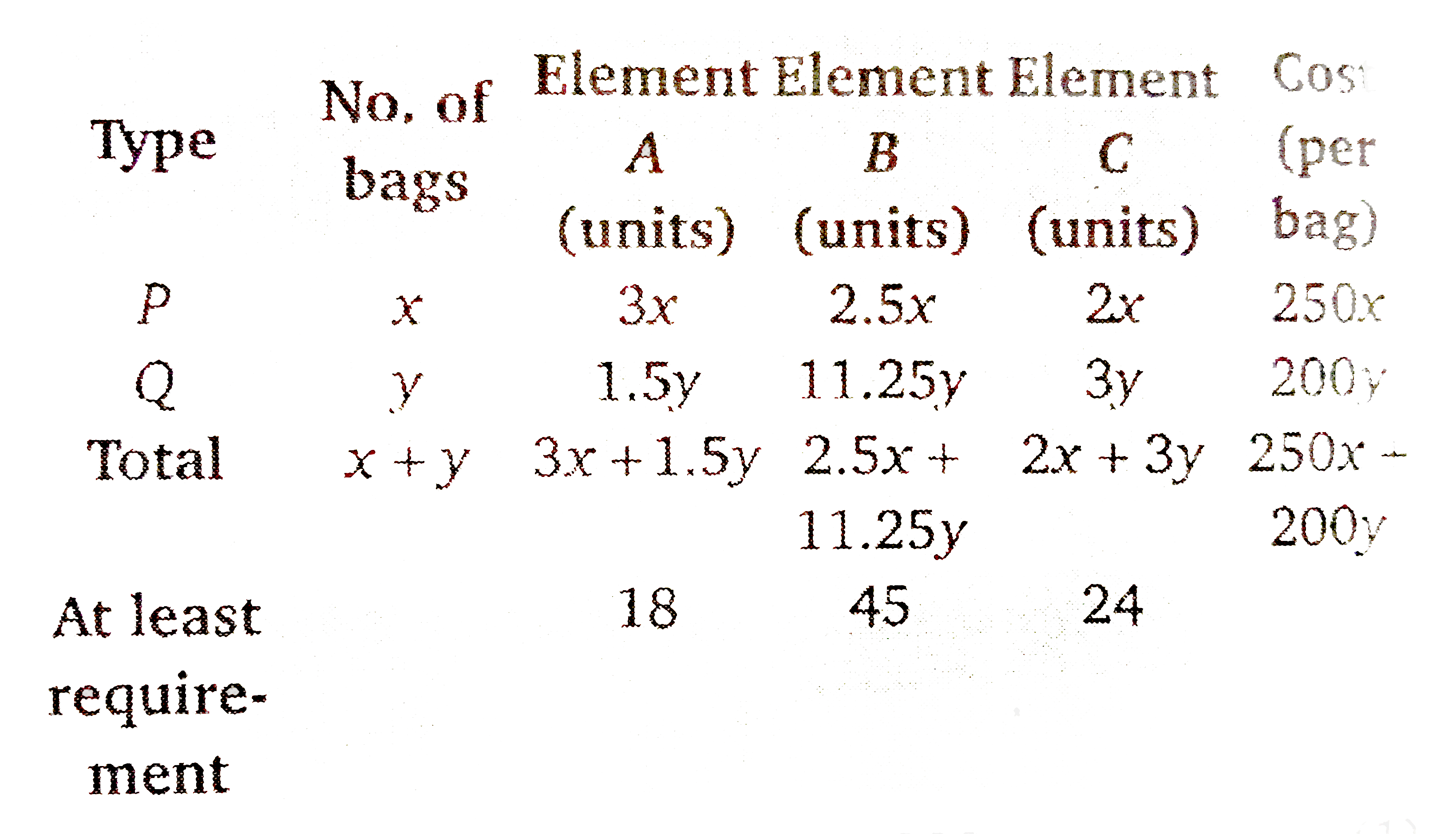
Minimise $Z = 250 x + 200 y$ …………..1
and constraints
$3 x + 1.5 y \geq 18 \Rightarrow 2 x + y \geq 12$ …………2
$2.5 x + 11.25 y \geq 45 \Rightarrow 2 x + 9 y \geq 36$ ….............3
$2 x + 3 y \geq 24$ ...................4
$x \geq 0, y \geq 0$ ...................5
First draw the graph of the line $2 x + y = 12$

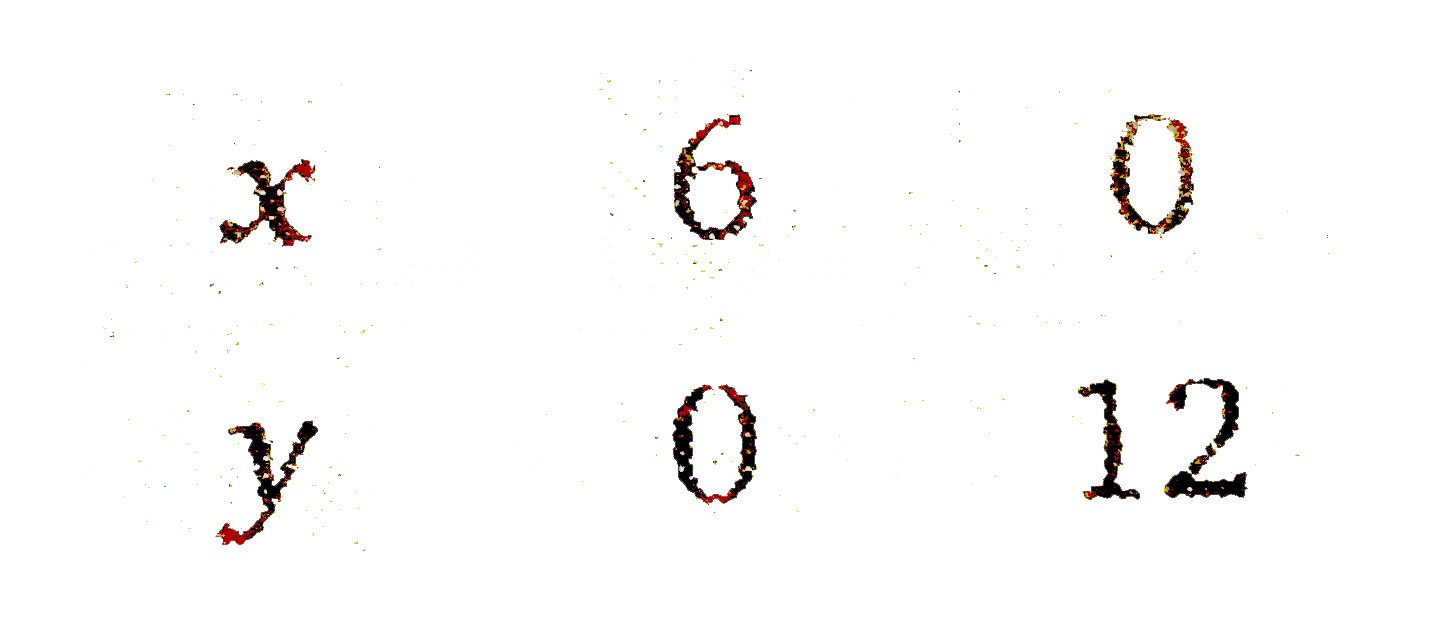
Put $(0, 0)$ in the inequation $2 x + y \geq 12$ ,
$2 \times 0 + 0 \geq 12 \Rightarrow 0 \geq 12$ (False)
Therefore, the half plane does not contain the origin.
Now, draw the graph of the line $2 x + 9 y = 36$ .

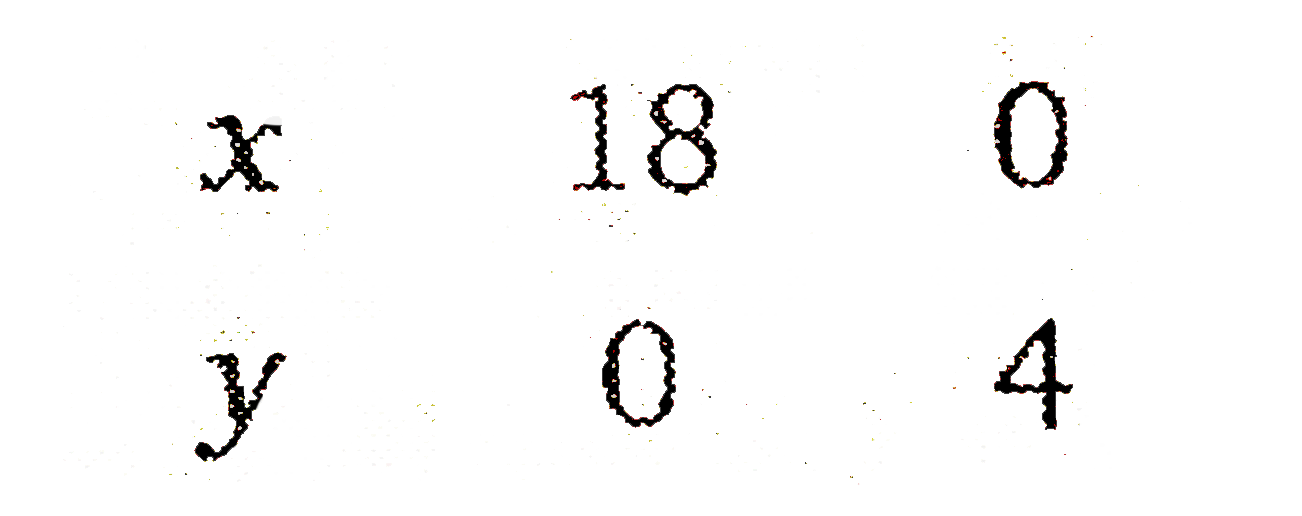
Put $(0, 0)$ in the inequation $2 x + 9 y \geq 36$ ,
$2 \times 0 + 9 \times 0 \geq 36 \Rightarrow 0 \geq 36$ (False)
Therefore the half plane does not contain the origin.
Now, draw the graph of the line $2 x + 3 y = 24$

Put $(0, 0)$ in the inequation $2 x + 3 y \geq 24$ ,
$2 \times 0 + 3 \times 0 \geq 40 > 2 \geq 24$ (False)
Thus, the half plane does not contain the origin,.
Since $x, y \geq 0$ so the feasible solution will be in first quadrant. From equations $3 x + 1.5 y = 18$ and $2 x + 3 y = 24$ the point of intersection is $C (3, 6)$ .
Similarly, the point of intersection of the equations $2.5 x + 11.25 y = 45$ and $2 x + 3 y = 24$ is $B (9, 2)$ . Thus, the vertices of the feasible region are $A (18, 0), B (9, 2), C (3, 6)$ and $D (0, 12)$ . We find the value of $Z$ at these vertices.

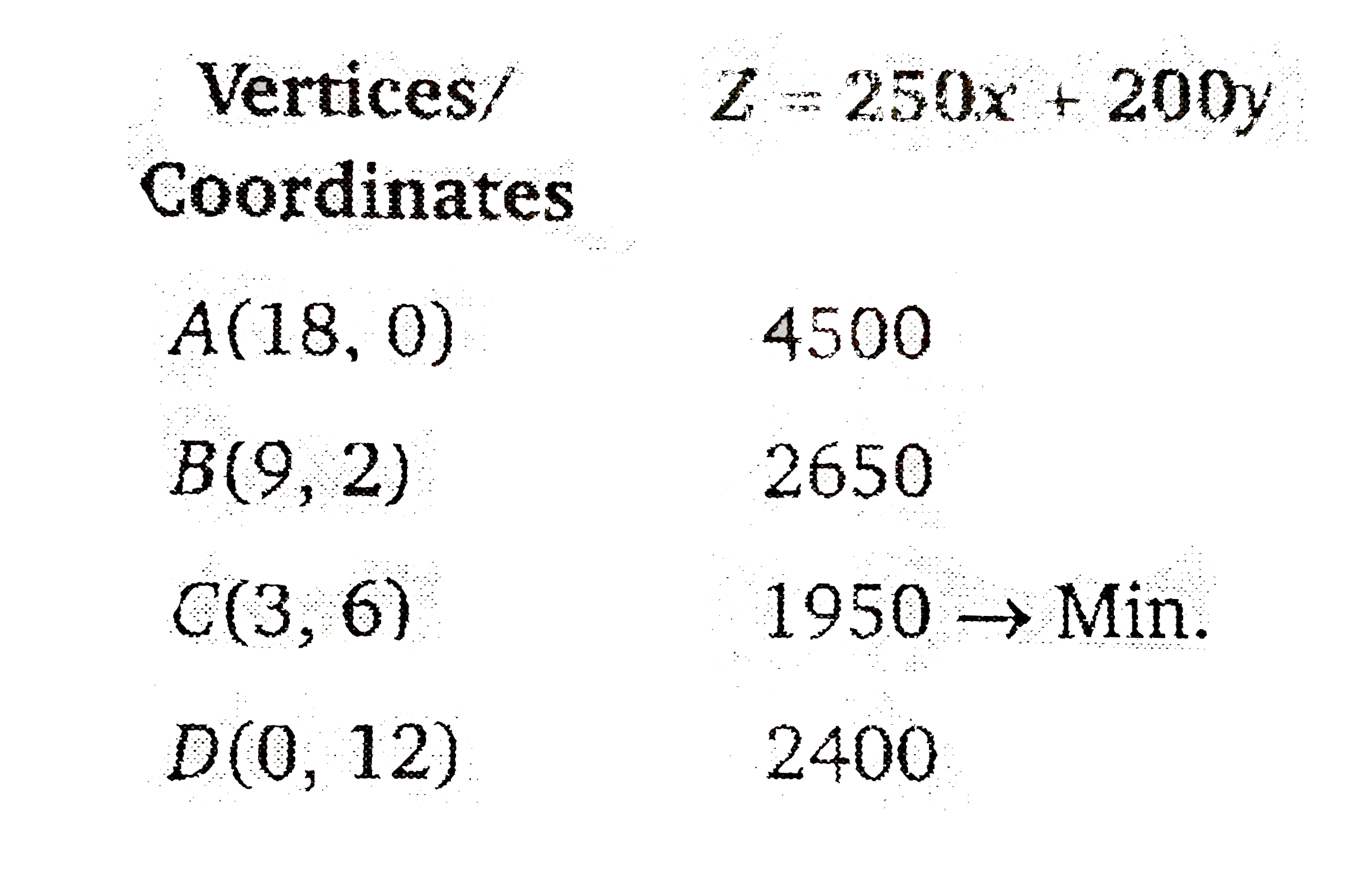
Since the feasible region is unbounded, so the minimum value of $Z$ may or may not be 1950. For this we draw the graph of inequation $250 x + 200 y < 1950$ or $5 x + 4 y 39$ . There is no common point here. Therefore minimum value of $Z$ is 1950 at point $C (3, 6)$ . Therefore, minimum cost is Rs. 1950 which is obtained by using 3 bags of type $P$ and 6 bags of type $Q$ cattle feed.

Updated on:21/07/2023

Food X contains 4 units of vitamin A per gram and 7 units of vitamin B per gram and cost 15 paise per gram . Food Y contains 6 units of vitamin A per gram and 11 units of vitamin B per gram and cost 22 paise per gram . The daily minimum requirement of vitamin A and B are 90 units and 130 units respectively . The formulation of LPP to minimize the cost is
Az = 15x +22y, subject to constraints $4 x + 6 y \geq 90, 7 x + 11 y \geq 130, x \geq 0 y \geq 0$
Bz = 6x +5y, subject to constraints $4 x + 3 y \geq 90, 7 x + 11 y \geq 130, x \geq 0 y \geq 0$
Cz = 15x +62y, subject to constraints $4 x + 6 y \geq 90, 7 x + 11 y \geq 450, x \geq 0 y \geq 0$
Dz = 15x +22y, subject to constraints $4 x + 6 y \geq 90, 7 x + 45 y \geq 260, x \geq 0 y \geq 0$
The unit of current element is ampere-metre. Find the dimensions of curent element.
A $[A M L]$
B $[A M L^{2} T]$
C $[M L T^{2}]$
D $[A L]$
The electonegativities of elements A and B are 1.2 and 3.4 units respectively the type of bond connecting A and B in compound AB is
Acovalent
Bionic
Ccoordinate covalent
Dpolar covalent