A feasible region of a system of linear inequalities is said to be ..., if it can be enclosed within a circle.
The correct Answer is:N/a
Step-by-Step Solution:
1. Understanding the Concept: A feasible region is the set of all possible points that satisfy a given system of linear inequalities.
2. Definition of Bounded Feasible Region: A feasible region is considered bounded if there is a limit to how far the points in the region can extend.
3. Circle Enclosure: If a feasible region can be enclosed within a circle, it means that all points of the region are contained within a finite distance from a central point.
4. Conclusion: Therefore, a feasible region that can be enclosed within a circle is termed as a "bounded feasible region".
Final Answer: A feasible region of a system of linear inequalities is said to be bounded if it can be enclosed within a circle.
---
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - TRUE/FALSE
2 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - OBJECTIVE
8 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
Knowledge Check
The solution set of system of linear inequalities 2(x+1)≤x+5,3(x+2)>2−x,x∈R is
A[−1,3]B(−1,3)C(−1,3]D[−1,3)The solution of system of linear inequalities in x represented on line as

(i) x∈(−∞,−4)∪[3,∞)
(ii) x∈(−∞,−4]∪(5,∞)
(iii) x∈(−∞,−3)∪(5,∞)
(iv) x∈(−∞,−4)∪[5,∞)Ax∈(−∞,−4)∪[3,∞)Bx∈(−∞,−4]∪(5,∞)Cx∈(−∞,−3)∪(5,∞)Dx∈(−∞,−4)∪[5,∞)
Solve the following systems of linear inequations:
1≤|x−2|≤3
View SolutionSolve the following system of linear inequalities graphically. x+y≥5 . . . (i)x−y≤3 . . . (ii)
View SolutionFind the linear inequalities for which the shaded region in the given figure is the solution set.
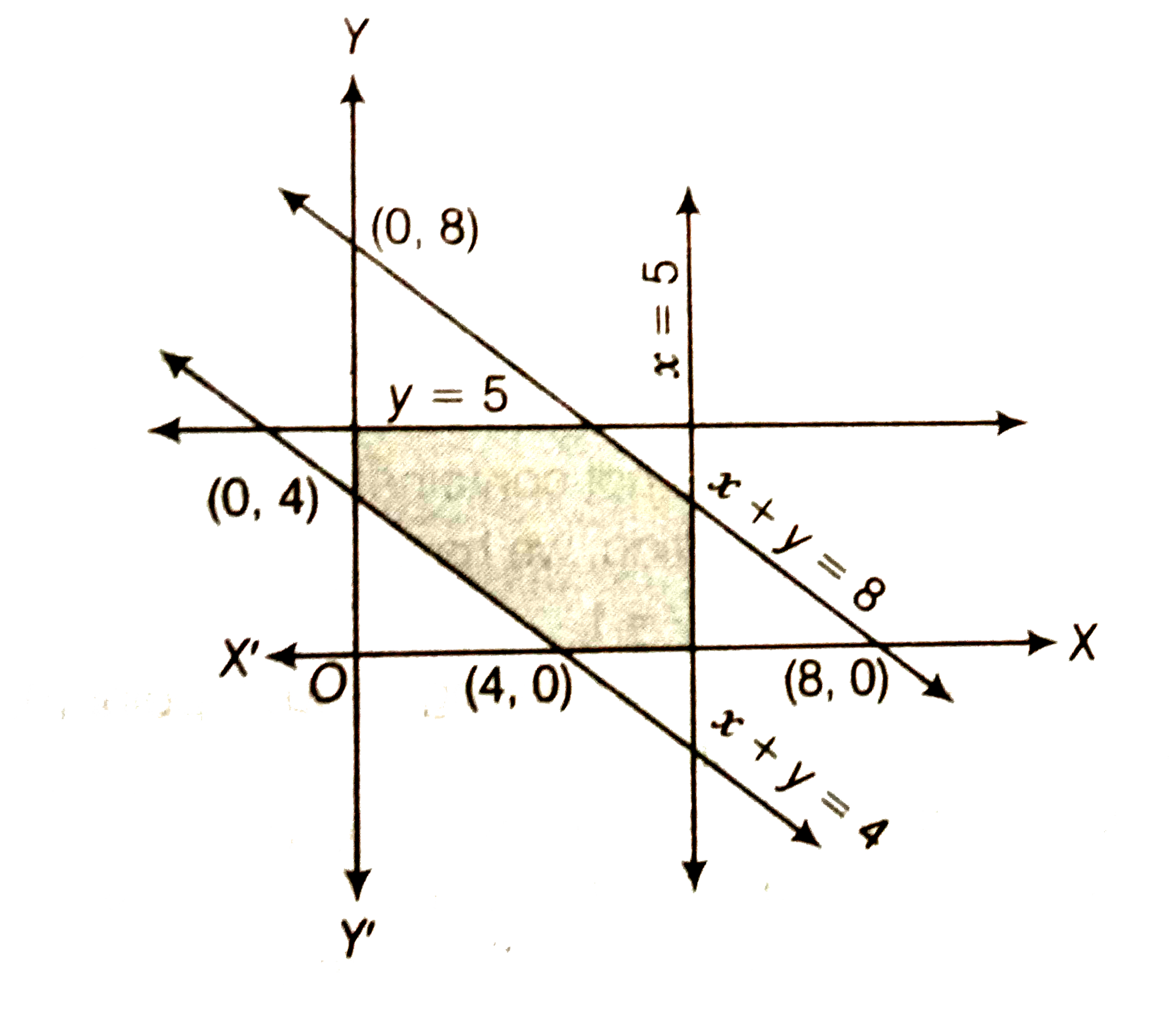
View SolutionFind the linear inequalities for which the shaded region in the given figure is the solution set.
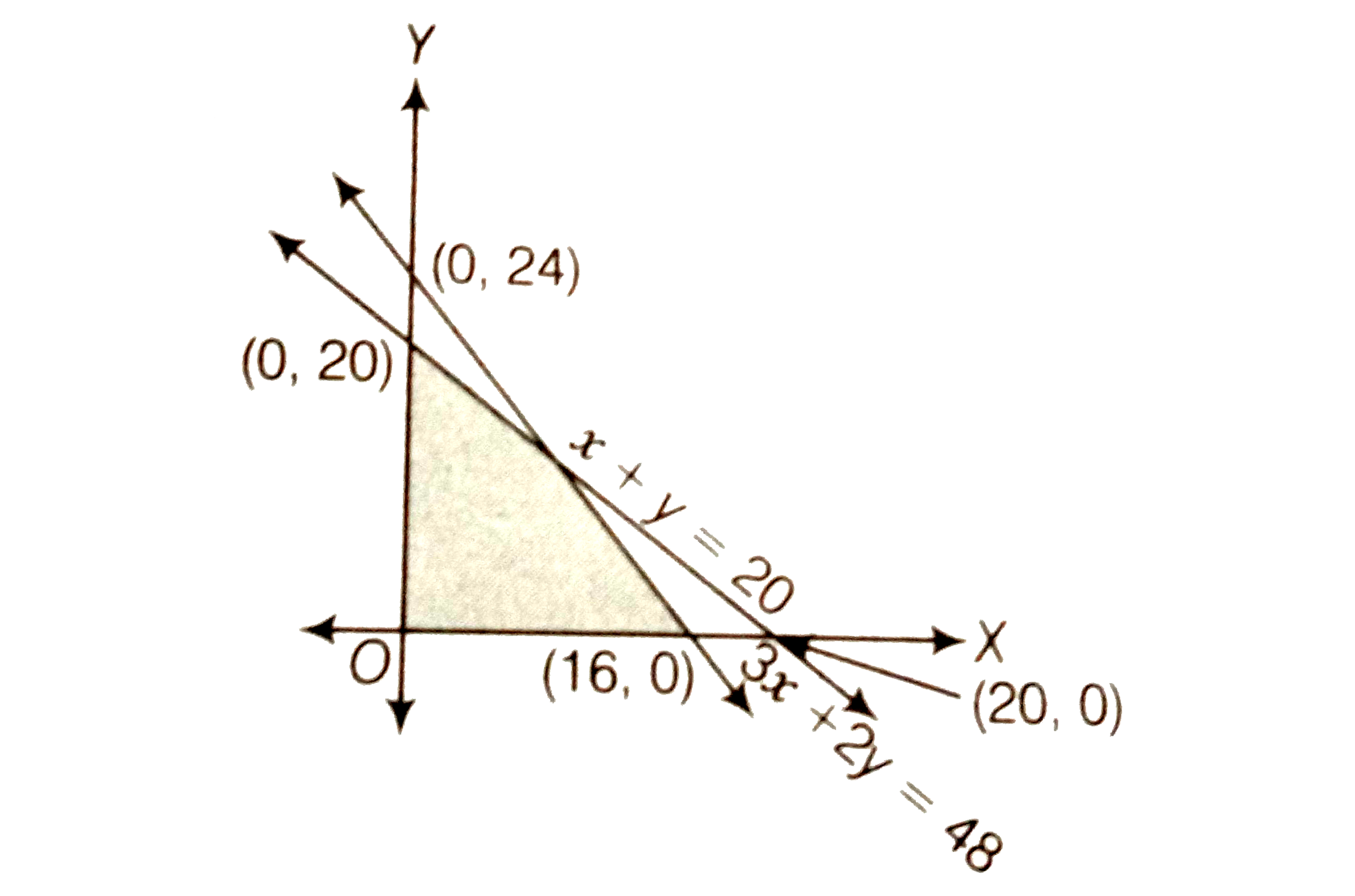
View SolutionShow that the solution set of the following system of linear inequalities is an unbounded region 2x+y≥8,x+2y≥10,x≥0,y≥0.
View SolutionIf (a, b) is a point in the solution region for the system of inequalities shown above and a=6, what is the minimu possible value of b?
√2⋅x56⋅x3√x
View Solution
