A function satisfies g(5)=3 and g(3)=0, and a function h satisfies h(3)=-2 and h(0)=5.What is the value of h(g(3))?
To solve the problem step by step, we need to evaluate the expression h(g(3)) using the information provided about the functions g and h.
Step 1: Find g(3)
From the problem, we know that:
g(3)=0
This means that when we input 3 into the function g, the output is 0.
Hint: Look for the value of g(3) directly from the information given.
Step 2: Substitute g(3) into h
Now that we have g(3)=0, we can substitute this value into the function h:
h(g(3))=h(0)
Hint: Replace g(3) with its value to simplify the expression.
Step 3: Find h(0)
Next, we need to find the value of h(0). From the problem, we know that:
h(0)=5
Hint: Look for the value of h(0) in the information provided.
Step 4: Conclusion
Now we can conclude that:
h(g(3))=h(0)=5
Thus, the final answer is:
5
From the problem, we know that:
g(3)=0
This means that when we input 3 into the function g, the output is 0.
Now that we have g(3)=0, we can substitute this value into the function h:
h(g(3))=h(0)
Next, we need to find the value of h(0). From the problem, we know that:
h(0)=5
Now we can conclude that:
h(g(3))=h(0)=5
5
Topper's Solved these Questions
Similar Questions
Knowledge Check
A function f satisfies f (2) = 3 and f (3) = 5. A function g satisfies g(3) = 2 and g(5) = 6. What is the value of f(g(3)) ?
A2B3C5D6IF the function g is defined by g(x)=3x+5, what is the value of g(-5)?
A-20B-10C20D60g(x)=2x-1
h(x)=1-g(x)
The functions g and h are defined above. What is the value of h(0) ?A−2B0C1D2
The function f(x)=x+1x3+1 can be written as the sum of an even function g(x) and an odd function h(x) . Then the value of |g(0)| is___________
View Solution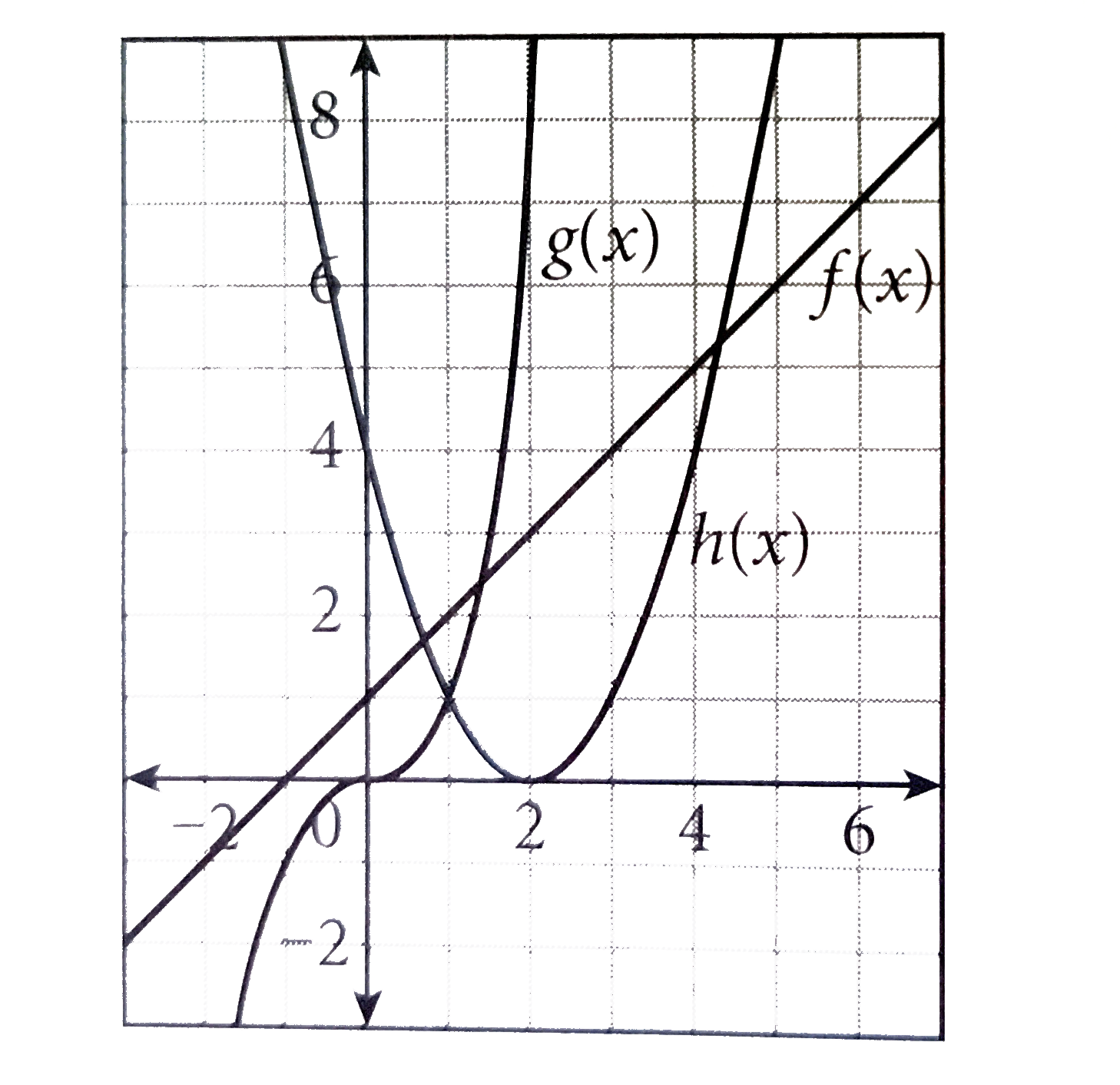
In the figure above, what is the value of h(0)−3(g(1)−f(2)) ?
View SolutionIf f(x) be a function such that f(−x)=−f(x),g(x) be a function such that g(−x)=−g(x) and h(x) be a function such that h(−x)=h(x), then choose the correct statement:
I. h(f(g(−x)))=−h(f(g(x)))
II. f(g(h(−x)))=f(g(h(x)))
III. g(f(−x))=g(f(x))
View Solution
Several values for the functions g (x) and h (x) are shown in the table above. What is the value of g(h(3)) ?
View Solutionh(x)=2x
The function h is defined above. What is h(5) − h( 3) ?
View Solution
