A line cuts two sides AB and AC of ΔABC at points P and Q respectively. Prove A(ΔAPQ)A(ΔABC)=AP×AQAB×AC.
NA
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE
15 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - SUBJECTIVE TYPE
20 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - EXAMPLE TYPE
50 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
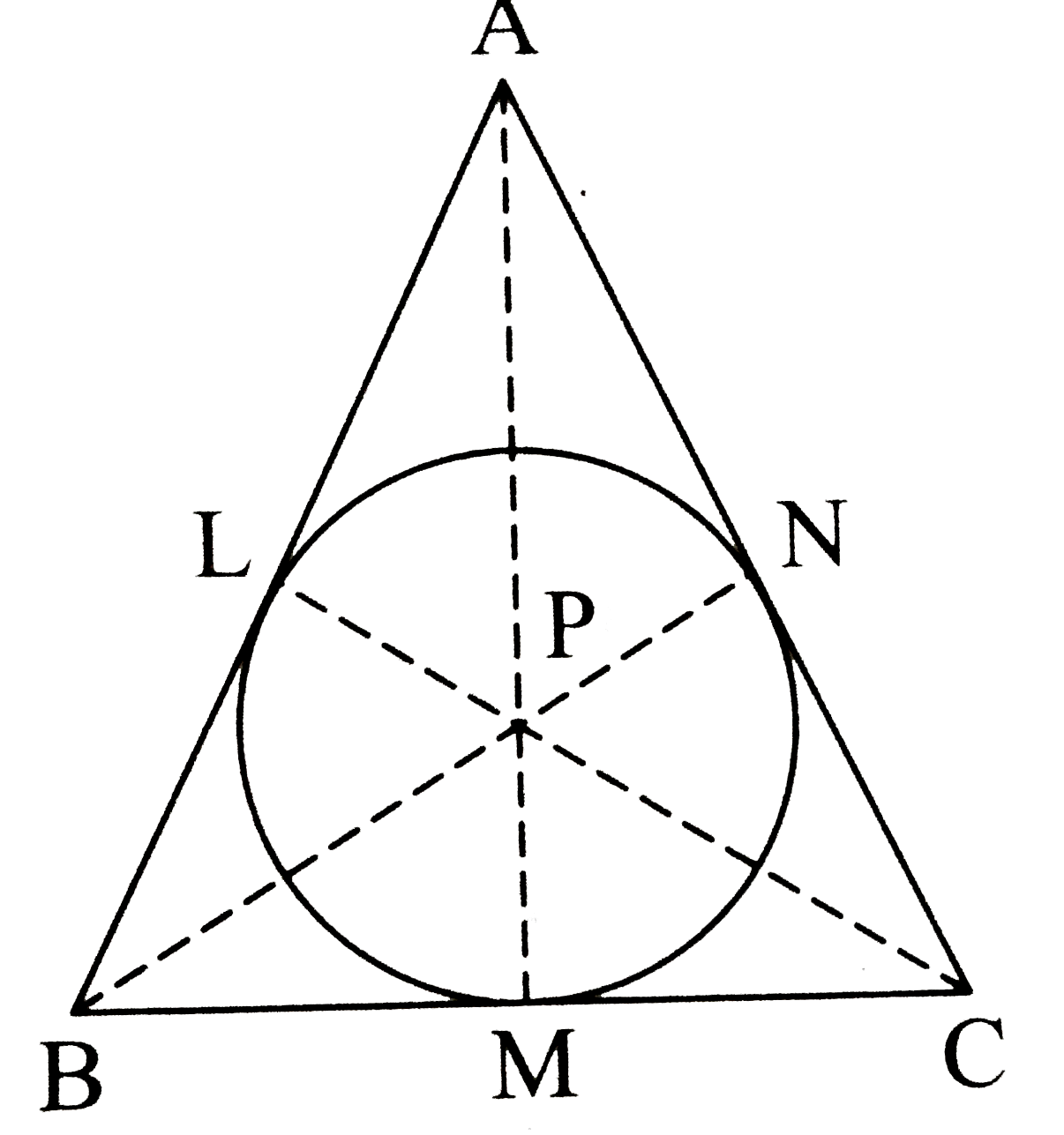
A circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View SolutionThe vertices of a ΔABC are A(3,0),B(0,6)andC(6,9). A straight line DE divides AB and AC in the ration 1:2 at D and E respectively, prove that ΔABCΔADE=9
View Solution
Knowledge Check
The mid points of AB and AC of the ΔABC are P and Q respectively. If PQ=6cm, then the side BC is
A10 cm.B12 cm.C8 cm.D14 cm.Mid-points of the sides AB and AC of a ΔABC are (3, 5) and (-3, -3) respectively, then the length of the side BC is
A10 unitB20 unitC15 unitD30 unitMid-points of the sides AB and AC of a ΔABC are (3, 5) and (-3, -3) respectively, then the length of the side BC is
A10 unitB20 unitC15 unitD30 unit
A circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. Prove that AQ=1/2(Perimeter of ΔABC).
View SolutionIn the given figure, the sides AB and AC of ΔABC have been extended to D and E respectively. If x>y, show that AB>AC.

View SolutionLine m intersects sides AB and AC of ΔABC in the points P and Q respectively. AP=4.2,PB=6.3,AQ=4,QC=6. State with reason whether line m is parallel to side BC or not.
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG show that :
CDGH=ACFG
View SolutionMid points of the sides Ab and AC of a ΔABC are (3,5) and (-3,-3) respectively, then the length of the side BC is
View Solution
