In the given figure, the sides AB and AC of ΔABC have been extended to D and E respectively. If x>y, show that AB>AC.
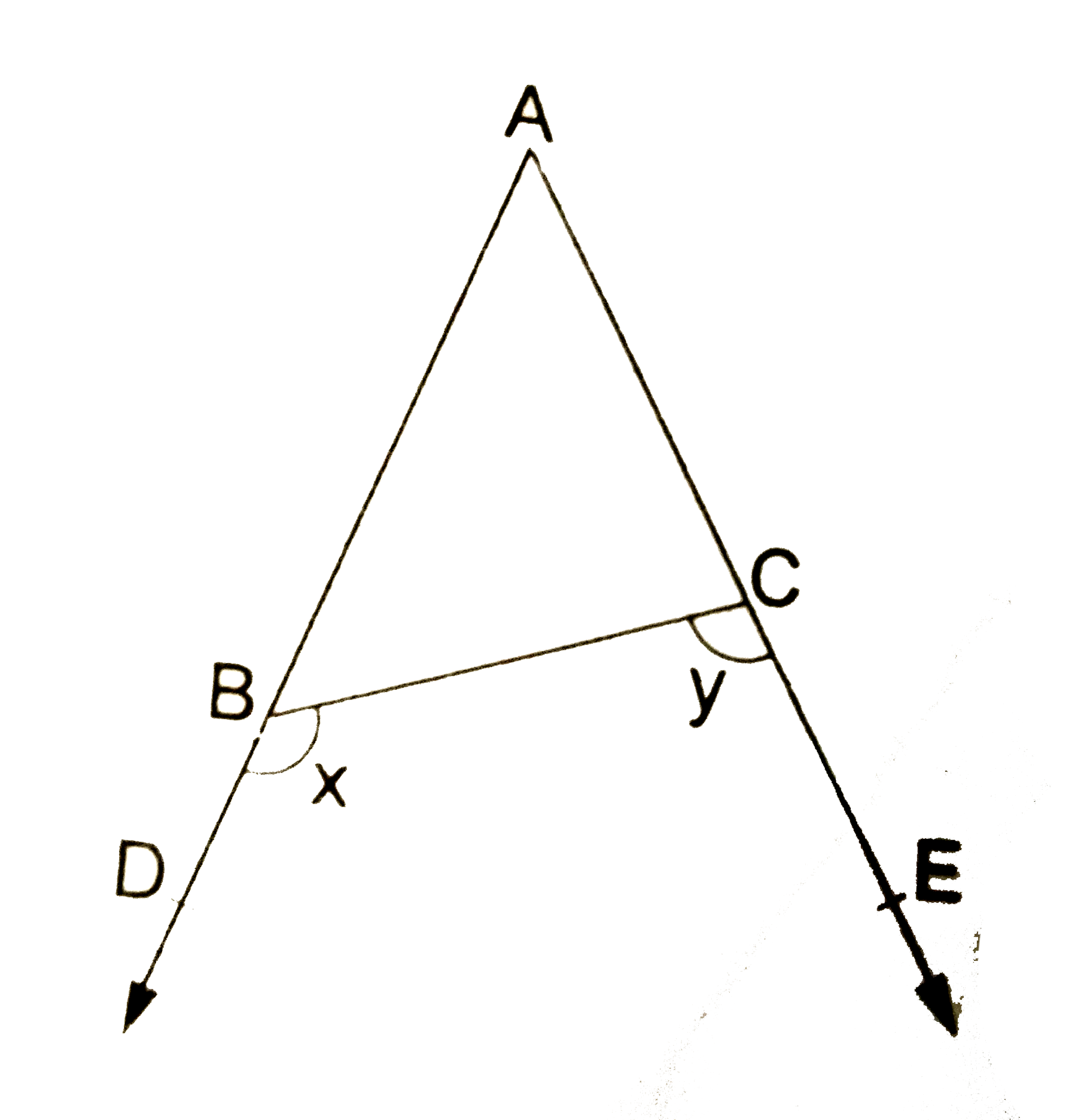
x>y⇒−x<−y
⇒ (180−x)(180−y)
⇒ ∠ABC<∠ACB
⇒ ∠ACB>∠ABC
⇒ AB>AC [side opposite to larger angle is larger].
Hence, AB>AC.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A27videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B16videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)37videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)22videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In triangle ABC , sides AB and AC are extended to D and E, respectively, such that AB=BD and AC =CE,F∈dDE,ifBC=6 cm.
A3 cmB6cmC9 cmD12 cm - Question 2 - Select One
The external bisector of ∠Band∠C of ΔABC(where AB and AC extended to E and F respectively) meet at point P. If ∠BAC=100∘, then the measure of ∠BPC is
A50∘B80∘C40∘D100∘ - Question 3 - Select One
Mid-points of the sides AB and AC of a ΔABC are (3, 5) and (-3, -3) respectively, then the length of the side BC is
A10 unitB20 unitC15 unitD30 unit
Let ABC be a given isosceles triangle with AB=AC . Sides ABandAC are extended up to EandF, respectively, such that BExCF=AB2. Prove that the line EF always passes through a fixed point.
View SolutionIn the given figure, △ABC is an isosceles triangle in which AB - AC. If AB and AC are produced to D and E respectively such that BD = CE, prove that BE = CD. Hint. Show that △ACD=△ABE.
 View Solution
View SolutionConsider a triangle ABC. The sides AB and AC are extended to points D and E respectively, such that AD=3ABandAE=3AC. Then one diagonal of BDEC divides the other diagonal in the ratio p:q then p+q=
View SolutionIf a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
View SolutionIn given figure, FE = AC, ΔABC≅ ____.
 View Solution
View Solution