A line of fixed length 2 units moves so that its ends are on the positive x-axis and that part of the line x+y=0 which lies in the second quadrant. Then the locus of the midpoint of the line has equation. Solution in Bengali
x2+5y2+4xy−1=0
x2+5y2+4xy+1=0
x2+5y2−4xy−1=0
x2+5y2−4xy−1=0
The correct Answer is:A
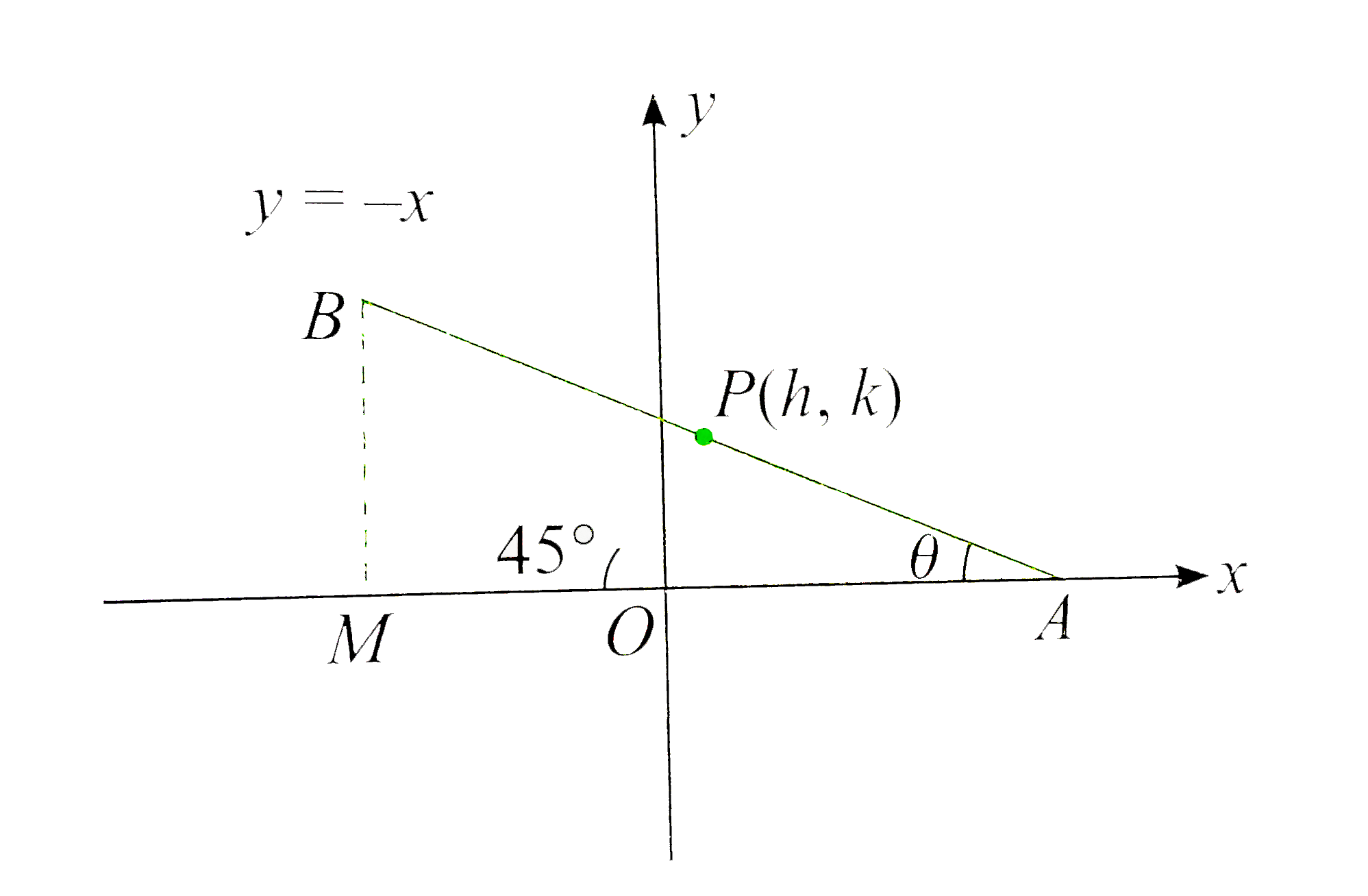
As shown in the figure, line segment AB, of fixed length 2 units, slides such that one of its ends A is on x-axis and other end B is on line x+y=0.
Let P(h,k) be midpoint of AB.
Also, let ∠BAO=θ.
So, in triangle AMB, BM = 2sinθ and AM=2cosθ.
In triangle BMO, MO=MB = 2sinθ
∴A≡(2cos θ−2sinθ,0) and B≡(−2 sinθ,2sin θ)
Now, P(h,k) is the midpoint of AB.
∴2h=2cos θ−2sinθ+(−2 sinθ) and 2k=2sin θ
⇒h=cos θ−2sinθ and k=sin θ
⇒h+2k=cos θ and k=sin θ
Squaring and adding, we get
(h+2k)2+k2=1
or x2+5y2+4xy−1=0
This is the required locus.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
05:07View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
04:21View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
02:32View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
03:27View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
08:20View SolutionA line of fixed length 2 units moves so that its ends are on the positive x-axis and that part of the line x+y=0 which lies in the second quadrant. Then the locus of the midpoint of the line has equation. (a) x2+5y2+4xy−1=0 (b) x2+5y2+4xy+1=0 (c) x2+5y2−4xy−1=0 (d) 4x2+5y2+4xy+1=0
05:53View SolutionFind the equation of the circle which is touched by y=x , has its center on the positive direction of the x=axis and cuts off a chord of length 2 units along the line √3y−x=0
06:29View SolutionFind the equation of the circle which touches the lines x=0,y=0andx=4 and lies in the first quadrant.
06:01View SolutionA line of length (a+b) unit moves in such a way that its ends are always on two fixed perpendicular striaght lines. Prove that the locus of a point on this line which divides it into of lenghts a unit and b unit is an ellipse.
05:21View SolutionA line of fixed length a + b moves so that its ends are always on two fixed perpendicular straight lines. Then the locus of a point which divides this line into portions of length a and b is
06:18View SolutionA line of fixed length 2 units moves so that its ends are on the positive x-axis and that part of the line x+y=0 which lies in the second quadrant. Then the locus of the midpoint of the line has equation. (a) x2+5y2+4xy−1=0 (b) x2+5y2+4xy+1=0 (c) x2+5y2−4xy−1=0 (d) 4x2+5y2+4xy+1=0
06:18View SolutionFind the equation of the circle which is touched by y=x , has its center on the positive direction of the x=axis and cuts off a chord of length 2 units along the line √3y−x=0
10:07View SolutionA line of fixed length 2 units moves so that its ends are on the positive x-axis and that part of the line x+y=0 which lies in the second quadrant. Then the locus of the midpoint of the line has equation.
03:35View SolutionFind the equation of the circle which is touched by y=x , has its center on the positive direction of the x=axis and cuts off a chord of length 2 units along the line √3y−x=0
01:23View SolutionA line AB of length '2l' moves with the end 'A' always on x - axis and the end 'B' on the line y = 6x find the equation of locus of middle point of AB
07:20View SolutionA line AB of length '2l' moves with the end 'A' always on x - axis and the end 'B' on the line y = 6x find the equation of locus of middle point of AB
07:20View Solution

