A missing helicopter is reported to have crashed somewhere in the rectangular region in Fig. 13.5. What is the probability that it is crashed inside the lake shown in the figure? (FIGURE)
To solve the problem, we need to find the probability that the helicopter crashed inside the lake, given that it crashed somewhere in a rectangular region. We will follow these steps:
Step 1: Determine the dimensions of the rectangular region
From the video transcript, we know the dimensions of the rectangular region are:
- Length = 9 km
- Width = 4.5 km
Step 2: Calculate the area of the rectangular region
The area A of a rectangle can be calculated using the formula:
A=Length×Width
Substituting the values:
Arectangle=9km×4.5km=40.5km2
Step 3: Determine the dimensions of the lake
From the transcript, we find the dimensions of the lake:
- Length = 3 km
- Width = 2.5 km
Step 4: Calculate the area of the lake
Using the same area formula:
Alake=Length×Width
Substituting the values:
Alake=3km×2.5km=7.5km2
Step 5: Calculate the probability that the helicopter crashed in the lake
The probability P that the helicopter crashed in the lake is given by the ratio of the area of the lake to the area of the rectangular region:
P=AlakeArectangle
Substituting the areas we calculated:
P=7.5km240.5km2
Calculating this gives:
P=7.540.5≈0.1852
Rounding to two decimal places, we find:
P≈0.18
Final Answer
The probability that the helicopter crashed inside the lake is approximately 0.18.
---
From the video transcript, we know the dimensions of the rectangular region are:
- Length = 9 km
- Width = 4.5 km
The area A of a rectangle can be calculated using the formula:
A=Length×Width
Substituting the values:
Arectangle=9km×4.5km=40.5km2
From the transcript, we find the dimensions of the lake:
- Length = 3 km
- Width = 2.5 km
Using the same area formula:
Alake=Length×Width
Substituting the values:
Alake=3km×2.5km=7.5km2
The probability P that the helicopter crashed in the lake is given by the ratio of the area of the lake to the area of the rectangular region:
P=AlakeArectangle
Substituting the areas we calculated:
P=7.5km240.5km2
Calculating this gives:
P=7.540.5≈0.1852
Rounding to two decimal places, we find:
P≈0.18
The probability that the helicopter crashed inside the lake is approximately 0.18.
Topper's Solved these Questions
Similar Questions
A missing helicopter is reported to have crashed somewhere in the rectangular region shown in Fig. 15.2. What is the probability that it crashed inside the lake shown in the figure?
View SolutionSuppose you drop a tie at random on the rectangular region shown in Fig. 13.14. What is the probability that it will land inside the circle with diameter 1 m? (FIGURE)
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, what is the average of the five angles shown inside the circle?
 A36B45C60D72
A36B45C60D72 - Question 2 - Select One
In the figure, ABCD is a rectangle and E is a point on the side AB. If AB=10andAD=5 what is the area of the shaded region in the figure?
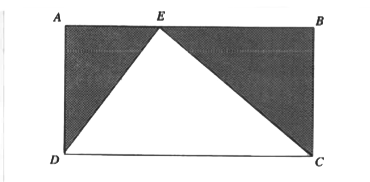 A25B30C35D40
A25B30C35D40
Suppose you drop a die at random on the rectangular region shown in Figure. What is the probability that it will land inside the circle with diameter 1m?
View SolutionIn figure, a dart is thrown and lands in the interior of the circle. What is the probability that the dart will land in the shaded region?
View SolutionIn the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
View SolutionA game of change consists of spinning an arrow which is equally likely to come to rest pointing to one of the number, 1, 2, 3, .., 12 as shown in Fig. 13.3. What is the probability that it will point to: (FIGURE) (i) 10? (ii) an odd number?
View SolutionIn the Figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
View SolutionThe triangles inside △ABC , shown above, are formed by joining the midpoints of the sides and then repeating the process. If a point is chosen at random inside △ABC ,what is the probability that the point lies in the shaded region ?
View Solution

