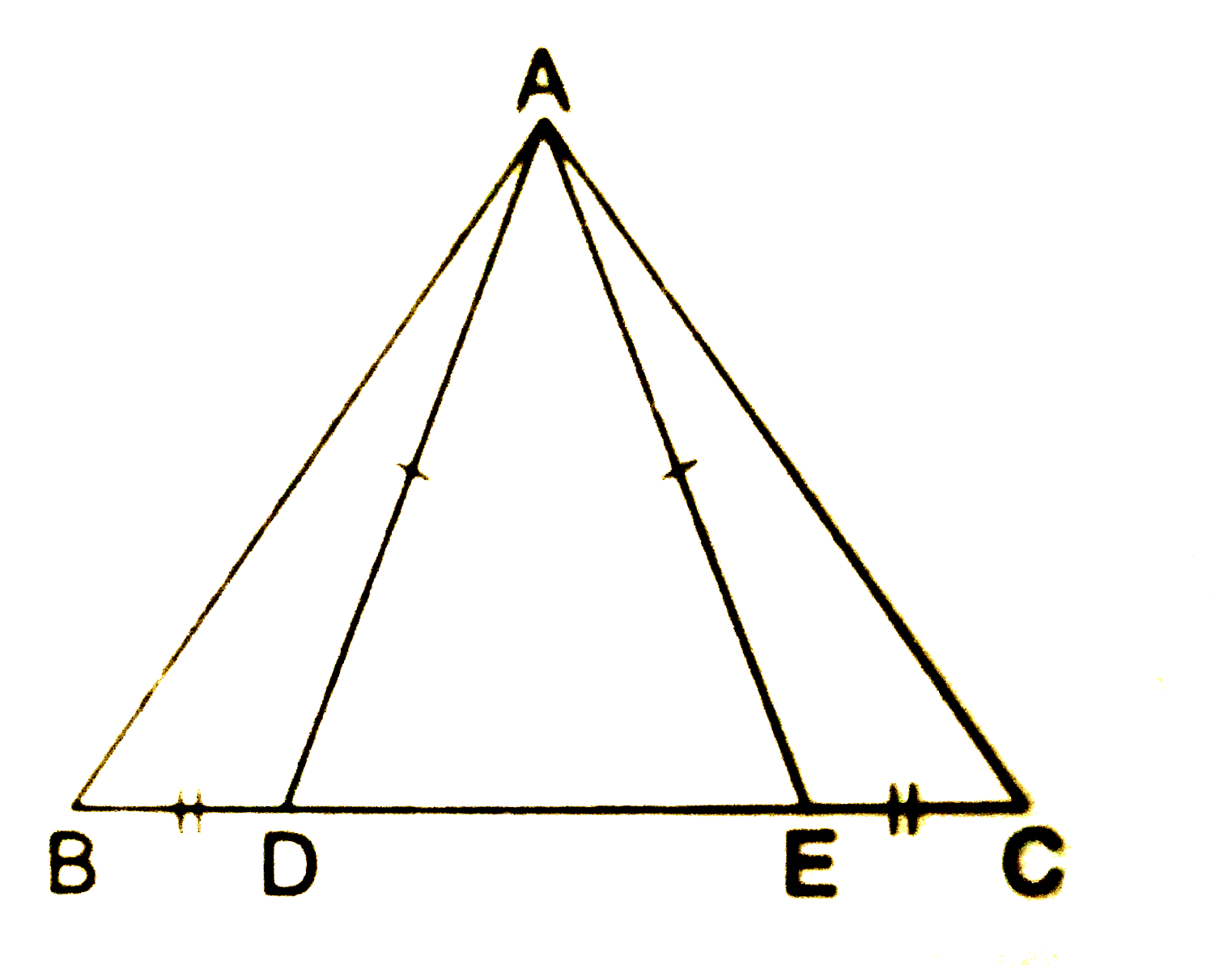
A point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
In ΔABC, we have BD=2DC
Let E is the mid-point of BD
Then, BE=ED=DC
Since, AE is the median of ΔABD
∴Ar(ΔABE)=ar(ΔAED)
(median divides the traingle into two equal areas) ...(1)
Also, since AD is the median of ΔAEC,
∴ar(ΔAED)=ar(ΔADC)
(median divides the triangle into two equal areas)...(2)
From eqs. (1) and (2), we have
ar(ΔABE)=ar(ΔAED)=ar(ΔADC)=x(say)
Now, ar(ΔABD)=ar(ΔABE)+ar(ΔAED)=x+x=2x=2×ar(ΔADC)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar12videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise34videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC,AD is the bisector of ∠A . Then , ar(ΔABD)ar(ΔACD)=
AAB2AC2BABACCBMCMDNone of these
A point D is on the side BC of an equilateral triangle ABC such that DC=14 BC . Prove that AD2=13 CD2 .
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View SolutionIn ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
View SolutionABCD is a trapezium with AB||DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).
View SolutionIn a ΔABC,BD is the median to the side Ac, BD is produced to E such that BD = DE. Prove that AE is parallel to BC.
View SolutionIn Fig. 30 D and E are to points on BC such that BD=DE=EC. Show that ar(ABD)=ar(ADE)=ar(AEC).
View Solution