A random variable X has the following probability distribution :
X:12345678P(X):0.150.230.120.100.200.080.070.08
for the events E=[X is a prime number] F={X<4}, the probability P(EUF), is.
To find the probability P(E∪F) where E is the event that X is a prime number and F is the event that X<4, we will follow these steps:
Step 1: Identify the prime numbers in the range of X
The prime numbers from the given random variable X (which takes values from 1 to 8) are:
- 2
- 3
- 5
- 7
Step 2: Calculate P(E)
We need to find the probability of event E (i.e., P(E)):
P(E)=P(X=2)+P(X=3)+P(X=5)+P(X=7)
Using the given probabilities:
- P(X=2)=0.23
- P(X=3)=0.12
- P(X=5)=0.20
- P(X=7)=0.07
Calculating:
P(E)=0.23+0.12+0.20+0.07=0.62
Step 3: Identify the values of X that are less than 4
The values of X that are less than 4 are:
- 1
- 2
- 3
Step 4: Calculate P(F)
Now we calculate the probability of event F (i.e., P(F)):
P(F)=P(X=1)+P(X=2)+P(X=3)
Using the given probabilities:
- P(X=1)=0.15
- P(X=2)=0.23
- P(X=3)=0.12
Calculating:
P(F)=0.15+0.23+0.12=0.50
Step 5: Calculate P(E∩F)
Next, we find the intersection of events E and F (i.e., P(E∩F)):
The prime numbers that are also less than 4 are:
- 2
- 3
Thus,
P(E∩F)=P(X=2)+P(X=3)=0.23+0.12=0.35
Step 6: Calculate P(E∪F)
Now we can use the formula for the union of two events:
P(E∪F)=P(E)+P(F)−P(E∩F)
Substituting the values we calculated:
P(E∪F)=0.62+0.50−0.35=0.77
Final Answer
Thus, the probability P(E∪F) is 0.77.
---
The prime numbers from the given random variable X (which takes values from 1 to 8) are:
- 2
- 3
- 5
- 7
We need to find the probability of event E (i.e., P(E)):
P(E)=P(X=2)+P(X=3)+P(X=5)+P(X=7)
Using the given probabilities:
- P(X=2)=0.23
- P(X=3)=0.12
- P(X=5)=0.20
- P(X=7)=0.07
P(E)=0.23+0.12+0.20+0.07=0.62
The values of X that are less than 4 are:
- 1
- 2
- 3
Now we calculate the probability of event F (i.e., P(F)):
P(F)=P(X=1)+P(X=2)+P(X=3)
Using the given probabilities:
- P(X=1)=0.15
- P(X=2)=0.23
- P(X=3)=0.12
P(F)=0.15+0.23+0.12=0.50
Next, we find the intersection of events E and F (i.e., P(E∩F)):
The prime numbers that are also less than 4 are:
- 2
- 3
P(E∩F)=P(X=2)+P(X=3)=0.23+0.12=0.35
Now we can use the formula for the union of two events:
P(E∪F)=P(E)+P(F)−P(E∩F)
Substituting the values we calculated:
P(E∪F)=0.62+0.50−0.35=0.77
Thus, the probability P(E∪F) is 0.77.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section I - Solved Mcqs39videos
DISCRETE PROBABILITY DISTRIBUTIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type1videos
DISCRETE PROBABILITY DISTRIBUTIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DETERMINANTSEXERCISE - Chapter Test30videos
DETERMINANTS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Chapter Test29videos
FUNCTIONS
Similar Questions
A random varibale X has the following probability distribution.
X:12345P(X):00.10.20.30.4
Find the mean.View SolutionFind the mean and variance for the following probability distribution: ∣∣∣xi1234pi0.40.30.20.1∣∣∣
View SolutionA random variable X has the following distribution
X=x1:−2−10123P(X=x1):0.1k0.22k0.3k
The value of k and its mean and variance areView SolutionA random variable X has the following probability distribution:
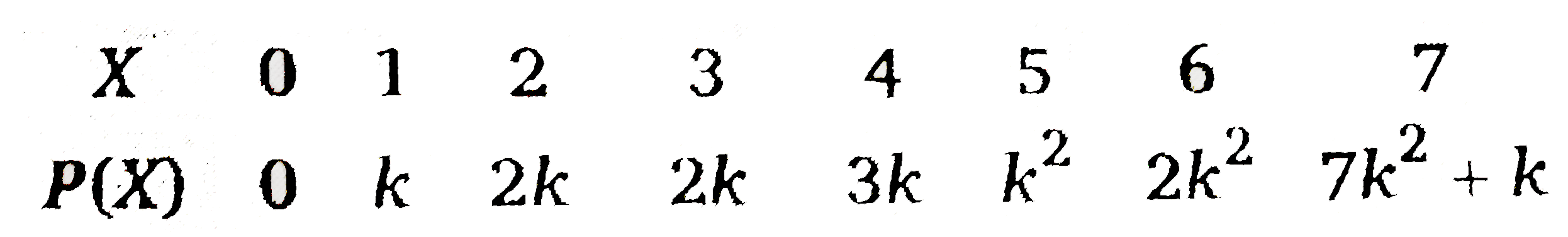
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)View SolutionA random variable has the following probability distribution: 1 2 3 4 5 6 7 8 For the events E=[X:X is a prime number], F={X:X<4} , the probability P(E∪F) is 0.50 b. 0.77 c. 0.35 d. 0.87
View SolutionA random variable X has the following probability distribution:
X: −2 −1 0 1 2 3
P(X):0.1 k 0.2 2k 0.3 k , find value of kView SolutionThe probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, isView SolutionA random variable has the following distribution.
x=xi−3−2−1012P(x=xi)0.12K3K7K0.20.1
Then for the values, A = K, B = Mean, C = Variance, the ascending order isView SolutionA random variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 , P (X): 0 K 2K 2K 3K K2 2K2 7K2+K Determine: (i) K (ii) P(X<3) (iii) P(X > 6) (iv) P (0 < X < 3)
View SolutionConsider the following assignments of probabilities for outcomes of sample space S = {1, 2, 3, 4, 5, 6, 7, 8}.
Number (X)12345678Probability, P(X)0.150.230.120.100.200.080.070.05
Find the probability that
X is a prime number
(b) X is a number greater than 4.View Solution
