The probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, is
1.76
2.45
3.2
4.8
The correct Answer is:A
To find the variance of the random variable X given its probability distribution, we can follow these steps:
Step 1: List the values and probabilities
The values of X and their corresponding probabilities are:
- X=0, P(X=0)=0.4
- X=1, P(X=1)=0.3
- X=2, P(X=2)=0.1
- X=3, P(X=3)=0.1
- X=4, P(X=4)=0.1
Step 2: Create a table for calculations
We will create a table to calculate X2⋅P(X) and X⋅P(X):
| X | P(X) | X2 | X2⋅P(X) | X⋅P(X) |
|-------|----------|---------|---------------------|-------------------|
| 0 | 0.4 | 0 | 02⋅0.4=0 | 0⋅0.4=0 |
| 1 | 0.3 | 1 | 12⋅0.3=0.3 | 1⋅0.3=0.3 |
| 2 | 0.1 | 4 | 22⋅0.1=0.4 | 2⋅0.1=0.2 |
| 3 | 0.1 | 9 | 32⋅0.1=0.9 | 3⋅0.1=0.3 |
| 4 | 0.1 | 16 | 42⋅0.1=1.6 | 4⋅0.1=0.4 |
Step 3: Calculate the summations
Now, we will calculate the summations needed for the variance formula.
1. Calculate ∑(X2⋅P(X)):
∑(X2⋅P(X))=0+0.3+0.4+0.9+1.6=3.2
2. Calculate ∑(X⋅P(X)):
∑(X⋅P(X))=0+0.3+0.2+0.3+0.4=1.2
Step 4: Calculate the variance
The formula for variance σ2 is:
σ2=∑(X2⋅P(X))−(∑(X⋅P(X)))2
Substituting the values we found:
σ2=3.2−(1.2)2
Calculating (1.2)2:
(1.2)2=1.44
Now substituting back:
σ2=3.2−1.44=1.76
Final Answer
The variance of X is σ2=1.76.
---
The values of X and their corresponding probabilities are:
- X=0, P(X=0)=0.4
- X=1, P(X=1)=0.3
- X=2, P(X=2)=0.1
- X=3, P(X=3)=0.1
- X=4, P(X=4)=0.1
We will create a table to calculate X2⋅P(X) and X⋅P(X):
|-------|----------|---------|---------------------|-------------------|
| 0 | 0.4 | 0 | 02⋅0.4=0 | 0⋅0.4=0 |
| 1 | 0.3 | 1 | 12⋅0.3=0.3 | 1⋅0.3=0.3 |
| 2 | 0.1 | 4 | 22⋅0.1=0.4 | 2⋅0.1=0.2 |
| 3 | 0.1 | 9 | 32⋅0.1=0.9 | 3⋅0.1=0.3 |
| 4 | 0.1 | 16 | 42⋅0.1=1.6 | 4⋅0.1=0.4 |
Now, we will calculate the summations needed for the variance formula.
∑(X2⋅P(X))=0+0.3+0.4+0.9+1.6=3.2
∑(X⋅P(X))=0+0.3+0.2+0.3+0.4=1.2
The formula for variance σ2 is:
σ2=∑(X2⋅P(X))−(∑(X⋅P(X)))2
Substituting the values we found:
σ2=3.2−(1.2)2
Calculating (1.2)2:
(1.2)2=1.44
Now substituting back:
σ2=3.2−1.44=1.76
The variance of X is σ2=1.76.
Topper's Solved these Questions
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type
1 Video
- DETERMINANTSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DETERMINANTSEXERCISE - Chapter Test
30 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Chapter Test
29 Videos
Similar Questions
X is a random variable with distribution given below
x:0123P(X=x):k3k3kk
The value of k and its variance are
View SolutionThe probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View SolutionThe probability distribution for a random variable X is as follows:
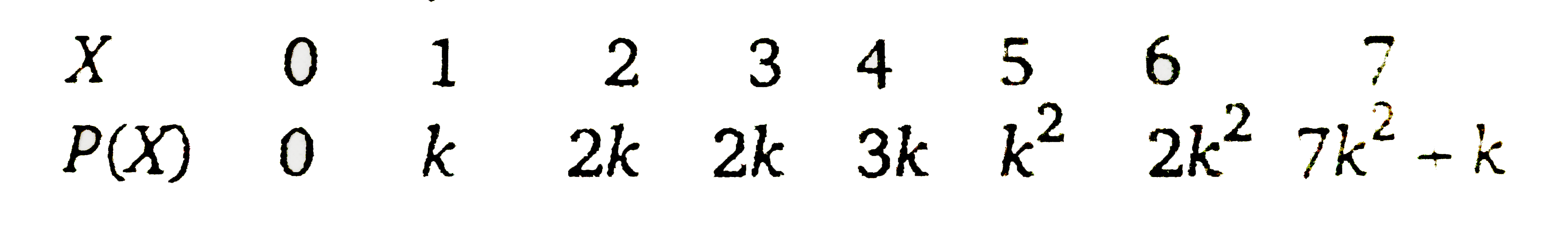
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionDetermine which of the following can be probability distributions of a random variable X: (i) X: 0 1 2 (ii) X: 0 1 2 P(X): 0.4 0.4 0.2 P(X): 0.6 0.1 0.2 (iii) X: 0 1 2 3 4 P(X): 0.1 0.5 0.2 -0.1 0.3
View SolutionThe probability distribution of a random variable (X) is P(X)={x12:X=1, 2, 3, 4, 5, 60:otherwise
Then, the conditional probability
P⎛⎝32<X<72X>2⎞⎠ is
View SolutionThe probability function of a random variable X is given by
p(x)=13, if x = -1, 0, 1
=0, otherwise.
Find the distribution function of X.
View SolutionA random variable X has the following probability distribution :
X:12345678P(X):0.150.230.120.100.200.080.070.08
for the events E=[X is a prime number] F={X<4}, the probability P(EUF), is.
View SolutionThe probability distribution function of a random variable X is given by xi:012 pi:3c34c−10c25c−1 Where c>0. Find : (i) c (ii) P(X<2) (iii) P(1<X≤2).
View SolutionDetermine which of the following can be probability distributions of a random variable X: X: 0 1 2 3 4 P(X): 0.1 0.5 0.2 −0.1 0.3
View Solution