A school has five houses A, B,C,D and E. A class has 23 students, 4 from houses A, 8 from house B and 5 from house C, 2 from house D and rest from house E. A single student is selected at random to be the class monitor. The probability that the selected student is not from A, B and C is
423
623
823
1723
The correct Answer is:B
To solve the problem, we need to find the probability that a randomly selected student is not from houses A, B, and C. Let's break down the solution step by step.
Step 1: Determine the total number of students
The total number of students in the class is given as 23.
Step 2: Identify the number of students from each house
- Students from house A = 4
- Students from house B = 8
- Students from house C = 5
- Students from house D = 2
- Students from house E = (Total students - Students from A, B, C, D)
First, we calculate the number of students from houses A, B, and C:
Total from A, B, C=4+8+5=17
Step 3: Calculate the number of students from house E
Now, we can find the number of students from house E:
Students from E=Total students−Total from A, B, C−Students from D
Students from E=23−17−2=4
Step 4: Determine the number of students not from A, B, and C
To find the number of students not from houses A, B, and C, we can add the students from houses D and E:
Students not from A, B, C=Students from D+Students from E
Students not from A, B, C=2+4=6
Step 5: Calculate the probability
The probability P that a randomly selected student is not from houses A, B, and C is given by the formula:
P(not from A, B, C)=Number of students not from A, B, CTotal number of students
P(not from A, B, C)=623
Final Answer
Thus, the probability that the selected student is not from houses A, B, and C is:
623
---
The total number of students in the class is given as 23.
- Students from house A = 4
- Students from house B = 8
- Students from house C = 5
- Students from house D = 2
- Students from house E = (Total students - Students from A, B, C, D)
Total from A, B, C=4+8+5=17
Now, we can find the number of students from house E:
Students from E=Total students−Total from A, B, C−Students from D
Students from E=23−17−2=4
To find the number of students not from houses A, B, and C, we can add the students from houses D and E:
Students not from A, B, C=Students from D+Students from E
Students not from A, B, C=2+4=6
The probability P that a randomly selected student is not from houses A, B, and C is given by the formula:
P(not from A, B, C)=Number of students not from A, B, CTotal number of students
P(not from A, B, C)=623
Thus, the probability that the selected student is not from houses A, B, and C is:
623
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - VERY SHORT ANSWERS QUESTIONS
14 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - SHORT ANSWERS QUESTIONS
42 Videos
- REAL NUMBERSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
In a medical examination of students of a class, the following blood groups are recorded.
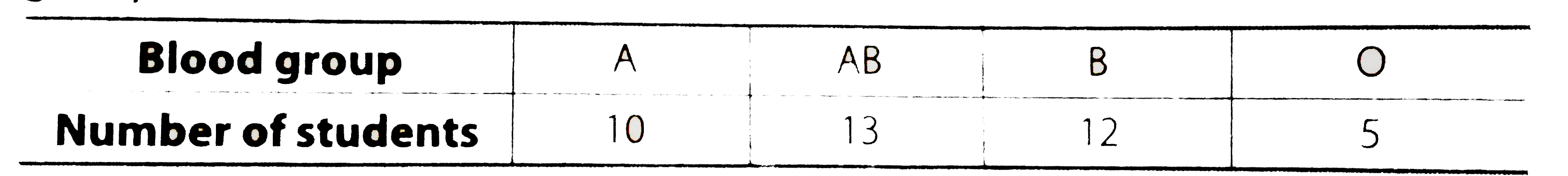
A student is selected at random from the class. The probability that he/she has blood group B, is
View SolutionA class consists of 50 students out of which there are 10 girls. In the class 2 girls and 5 boys are rank holders in an examination. If a student is selected at random from the class and is found to be a rank holder, what is the probability that the student selected is a girl?
View Solution
Knowledge Check
A class has 12 boys and 4 girls. If three students are selected at random from the class,
what is the probability that all will be boys?A155B14C13D1128The graph below shows the number of students who were present on Thursday from each of the 5 groups in Ms. Meagan's class. What is the probability that a student selected at random from the class on Thrusday is in Group 4?
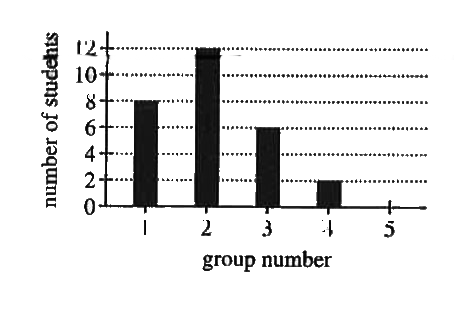 A128B114C15D14
A128B114C15D14
In Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
View SolutionIn class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both mathematics and biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology or both.
View SolutionOut of 32 students,8 are absent from the class. What is the percentage of the students who are absent?
View SolutionIn a class of 10 student, probability of exactly i students passing an examination is directly proportional to i2. If a student is selected at random, then the probability that he has passed the examination is
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passed in only one subject.
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passes in only one subject.
View Solution
