A square is incribed in an isoceles right triangle, so that the square and the triangle have one angle common. Show that the vertex of the sqare opposite the vertex of the common angle bisects the hypotenuse.
Given In isosceles traingle ABC, a square ADEF is inscribed.
To prove CE=BE
Proof In an isosceles ABC,
and
Since, ADEF is a square.
[all sides of square are equal]...(ii)
On subtracting Eq. (ii) from Eq. (i), we get
Now, in
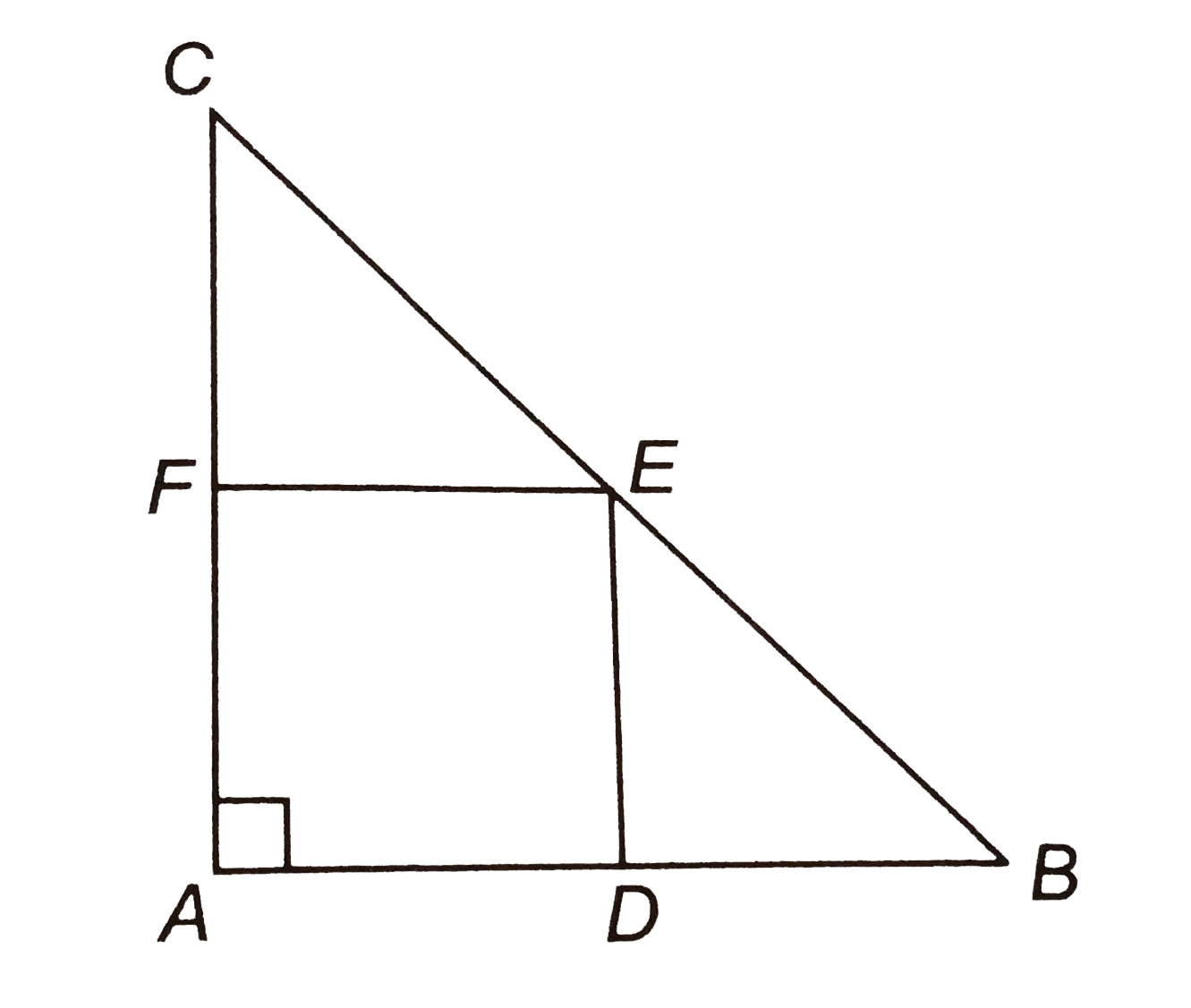
[from Eq. (iii)]
[sides of a square]
and [each ]
[by SAS congruence rule]
[by CPCT]
Hence, vertex E of the square bisects the hypotenuse BC.
Topper's Solved these Questions
Similar Questions
A square is inscribed in an isosceles right triangle so that the square and the triangle have an angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse
View SolutionA square is inscribed in a right-angled triangle with legs p and q, and has a common right angle with the triangle. The diagonal of the square is given by
View Solution
Knowledge Check
In a right-angled triangle, the square of the hypotenuse is equal to twice the product of the other two sides. One of the acute angles of the triangle is
A60∘B45∘C30∘D15∘In a right angled triangle, if sum of the squares of sides making right angle is 169 then what is the length of the hypotenuse ?
A15B13C5D12A square ABCD has an equilateral triangle drawn on the side AB ( interior of the square ) . The triangle has vertex at G. What is the measure of the angle CGB ?
A60∘B80∘C75∘D90∘
If perimeter of an isoceles right angled Δ is P . Then find the area of this triangle .
View SolutionIn a right triangle,Prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse
View SolutionIn a right angled triangle,if the sum of the squares of the sides making a right angle is 169, then what is the length of the hypotenuse?
View SolutionIf two isosceles triangles have a common base, prove that the line segment joining their vertices bisects the common base at right angles.
View SolutionProve that is a right angle triangle, the square of the hypotenuse is equal the sum of the squares of other two sides.
View Solution
