Question

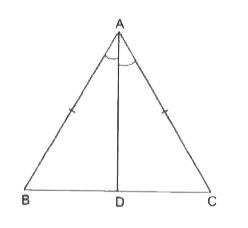
If two isosceles triangles have a common base, prove that the line segment joining their vertices bisects the common base at right angles.

Explanation

To prove that the line segment joining the vertices of two isosceles triangles with a common base bisects the base at right angles, we can follow these steps:

1. Identify the Triangles:
Let the two isosceles triangles be \( \triangle ABD \) and \( \triangle ACD \) with a common base \( BC \). Here, \( AB = AC \) and \( BD = CD \).

2. Label the Points:
Let \( A \) be the vertex of triangle \( ABD \) and \( D \) be the vertex of triangle \( ACD \). The common base is \( BC \).

3. Establish Congruence:
Since both triangles are isosceles, we have:
- \( AB = AC \) (sides of triangle \( ABD \) and \( ACD \))
- \( BD = CD \) (sides of triangle \( ABD \) and \( ACD \))
- \( AD = AD \) (common side)

4. Apply the SSS Congruence Criterion:
By the Side-Side-Side (SSS) congruence criterion, we can conclude:
\( \triangle ABD \cong \triangle ACD \)

5. Corresponding Angles are Equal:
Since the triangles are congruent, the corresponding angles are equal:
\( \angle BAD = \angle CAD \)

6. Sum of Angles on a Straight Line:
The angles \( \angle BAD \) and \( \angle CAD \) are adjacent angles on a straight line \( BC \). Therefore:
\( \angle BAD + \angle CAD = 180^\circ \)

7. Finding Right Angles:
Since \( \angle BAD = \angle CAD \), we can denote each angle as \( x \):
\( 2x = 180^\circ \implies x = 90^\circ \)
Thus, \( \angle BAD = \angle CAD = 90^\circ \).

8. Conclusion:
The line segment \( AD \) bisects the base \( BC \) at right angles, proving that \( AD \) is perpendicular to \( BC \).