A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the slops to form a box. What should be the side of the square to be cut off such that volume of the box is maximum possible .
Let the side of square be x and (0<x<9) , then the length of box is (18 - 2x), breadth is (18-2x) and height is x . Let V be the volume of the open box formed by folding the flaps of tin.
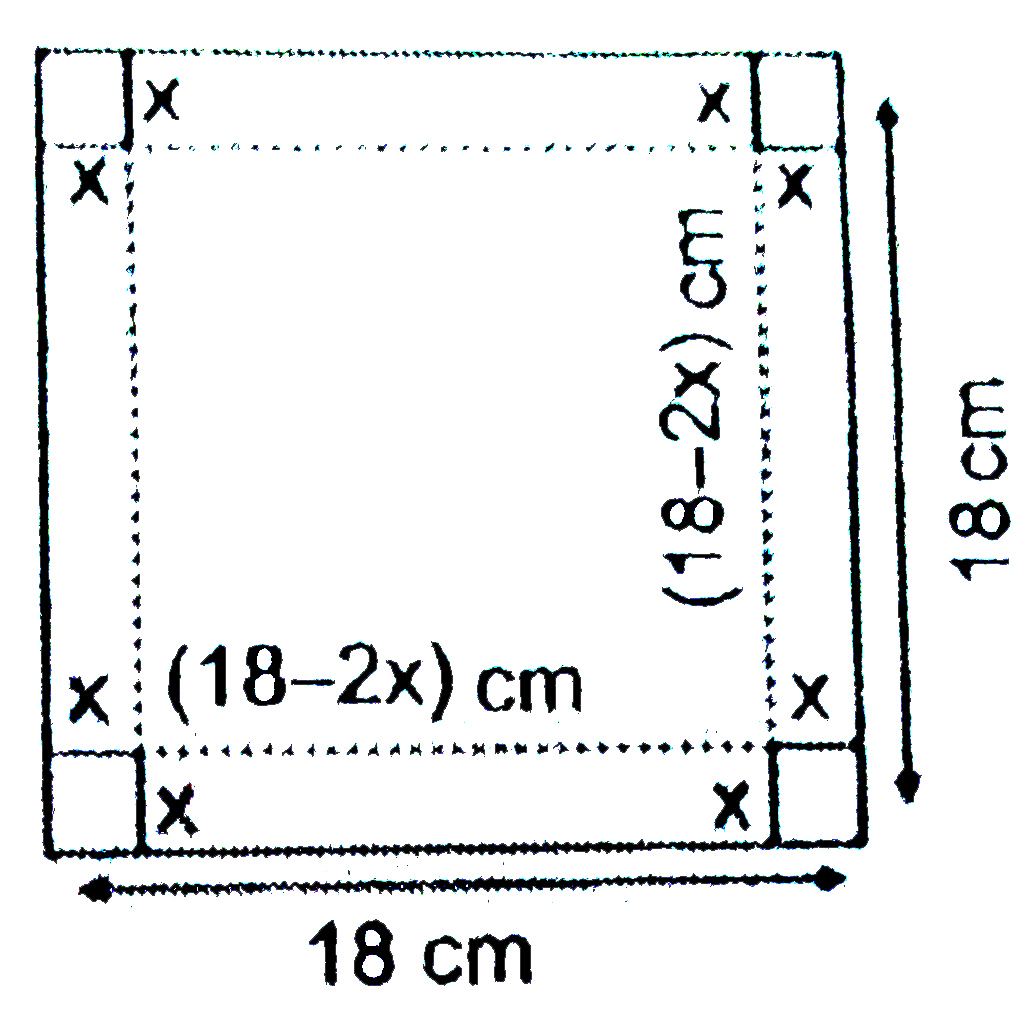
∴V=x(18−2x)(18−2x)
=4x(9−x)2=4x(81+x2−18x)
=4(x3−18x2+81x)
⇒dVdx=4(3x2−35x+81)=12(x2−12x+27)
and d2Vdx2=12(2x−12)=24(x−6)
For maximum value
dVdx=0⇒12(x2−12x+27)=0
⇒x2−12x+27=0
⇒(x−3)(x−9)=0
⇒x=3,9
but x = 9 is impossible so x = 3.
at x=3,(s2Vdx2)x=3=24(3−6)=−72<0
∴x=3
⇒ Side of square cut = 3 cm
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Miscellaneous Exercise
Explore 24 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 6.4
Explore 9 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHAN ENGLISHChapter:APPLICATIONS OF INTEGRALSExercise:Miscellaneous Exercise
Explore 19 Videos
Similar Questions
A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
View SolutionA square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Also, find the maximum volume.
View Solution
Knowledge Check

A square piece of cardbroad measuring x inches by x inches is to be used to form an open box by cutting off 2-inch squares, and then folding the slides up along the dotted lines, as shown in the figure above.
If x is an integer , and the volume of the box must be greater than 128 cubic inches , what is the smallest value of x that can be used ?A6B8C10D13
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top by cutting off squares from the corners and folding up the flaps. What should be the side of the square in order the volume of the box is maximum.
View SolutionA rectangular sheet of tin 58 cm×44cm is to be made into an open box by cutting off equal squares from the corners and folding up the flaps.What should be the volume of box if the surface area of box is 2452 cm2?
View SolutionA box of maximum volume with top open is to be made by cutting out four equal squares from four corners of a square tin sheet of side length a feet and then folding up the flaps. Find the side of the square cut-off.
View SolutionA wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
View SolutionA wire of length 36m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces, so that the combined area of the square and the circle is minimum?
View SolutionA wire of length 36m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces, so that the combined area of the square and the circle is minimum?
View SolutionThe side of a square is 6cm. A rectangle has the same perimeter as that of the square.
Find the area of the square.
View Solution