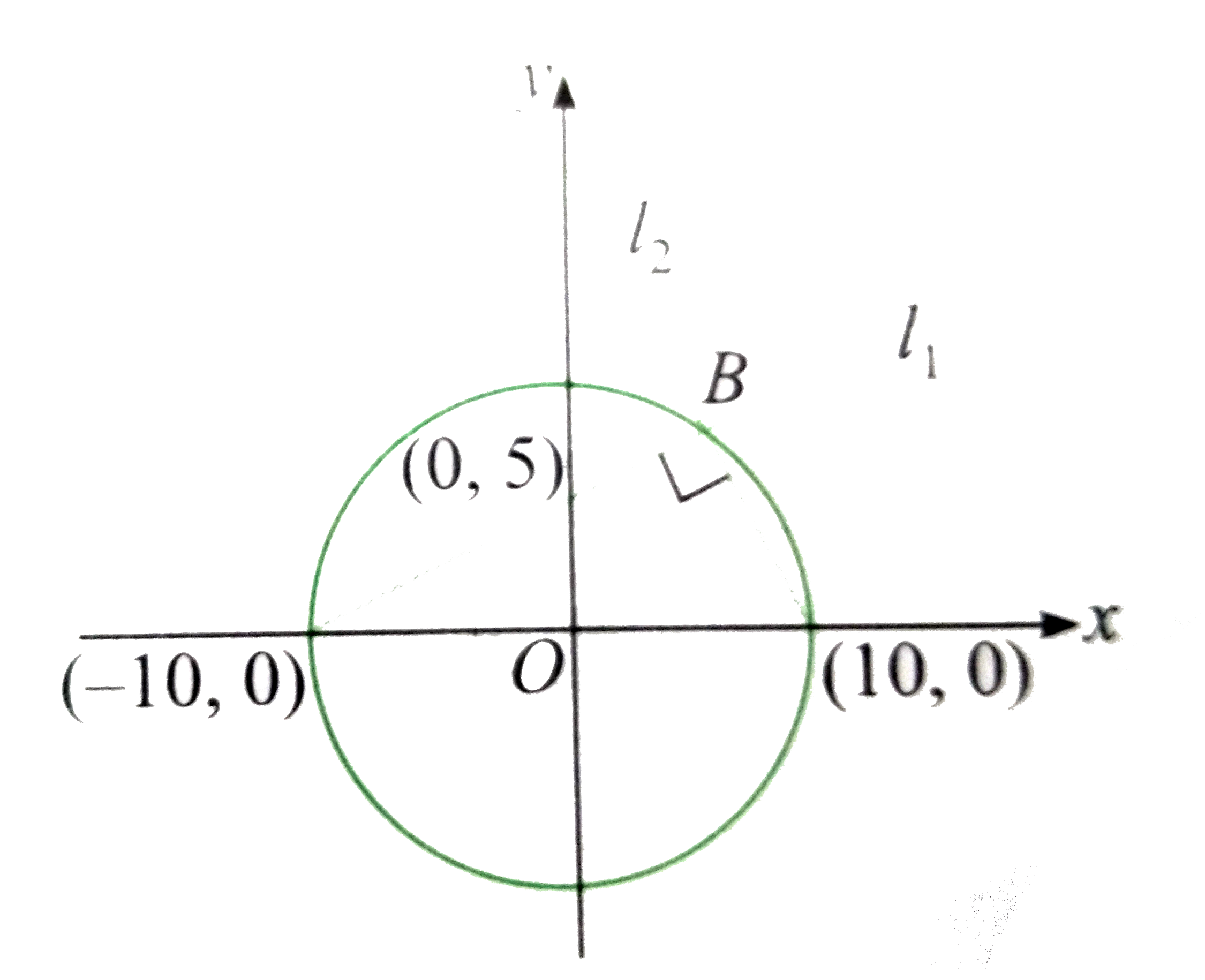
A straight line l1 with equation x−2y+10=0 meets the circle with equation x2+y2=100 at B in the first quadrant. A line through B perpendicular to l1 cuts the y-axis at P(o,t) . The value of t is 12 (b) 15 (c) 20 (d) 25Solution in Tamil
12
15
20
25
The correct Answer is:3
Slope of I1=12
Slope of I2=−2
The equation of I2 is
y=−2(x−10)
or y+2x=20
Hence, t=20
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven A≡(1,1) and AB is any line through it cutting the x-axis at B. If AC is perpendicular to AB and meets the y-axis in C , then the equation of the locus of midpoint P of BC is (a) x+y=1 (b) x+y=2 (c) x+y=2xy (d) 2x+2y=1
View SolutionA straight line l1 with equation x−2y+10=0 meets the circle with equation x2+y2=100 at B in the first quadrant. A line through B perpendicular to l1 cuts the y-axis at P(o,t) . The value of t is 12 (b) 15 (c) 20 (d) 25
View SolutionA given line L1 cut x and y-axes at PandQ respectively and has intercepts aandb2 on x and y-axes respectively. Let another line L2 perpendicular to L1 cut x and y-axes at RandS respectively. Let T be the point of intersection of PSandQR. Locus of T is a circle having centre at (A) (a,b) (B) (a,b2) (C) (a2,b) (D) (a2,b4)
View SolutionA given line L1 cut x and y-axes at PandQ respectively and has intercepts aandb2 on x and y-axes respectively. Let another line L2 perpendicular to L1 cut x and y-axes at RandS respectively. Let T be the point of intersection of PSandQR. A straight line passes through the centre of locus of T. Then locus of the foot of perpendicular to it from origin is : (A) a straight line (B) a circle (C) a parabola (D) none of these
View SolutionThe line xa−yb=1 meets the X-axis at P. Find the equation of the line perpendicular to this line at P.
View SolutionThe line (x)/(a)-(y)/(b) =1 cuts the x-axis at P. The equation of the line through P perpendicular to the given line is
View SolutionGiven A≡(1,1) and AB is any line through it cutting the x-axis at B. If AC is perpendicular to AB and meets the y-axis in C , then the equation of the locus of midpoint P of BC is (a) x+y=1 (b) x+y=2 (c) x+y=2xy (d) 2x+2y=1
View SolutionA straight line l1 with equation x−2y+10=0 meets the circle with equation x2+y2=100 at B in the first quadrant. A line through B perpendicular to l1 cuts the y-axis at P(0,t) . The value of t is (a)12 (b) 15 (c) 20 (d) 25
View SolutionGiven A≡(1,1) and AB is any line through it cutting the x-axis at B. If AC is perpendicular to AB and meets the y-axis in C , then the equation of the locus of midpoint P of BC is (a) x+y=1 (b) x+y=2 (c) x+y=2xy (d) 2x+2y=1
View Solutionthe line xa−yb=1 cuts the x-axes at P.the equation of the line passes through point P and perpendicular to the line is:
View SolutionThe line L1≡4X+3Y−12=0 intersects the x-and y-asxis at A and B, respectivly. A variable line perpendicular to L1 intersects the x-and y-axis at P and Q, respectively. Then the locus of the circumcenter of triangle ABQ is
View Solution
