A tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P&Q.Solution in Bengali
The given ellipse are
x24+y21=1 (1)
and x26+y23=1 (2)
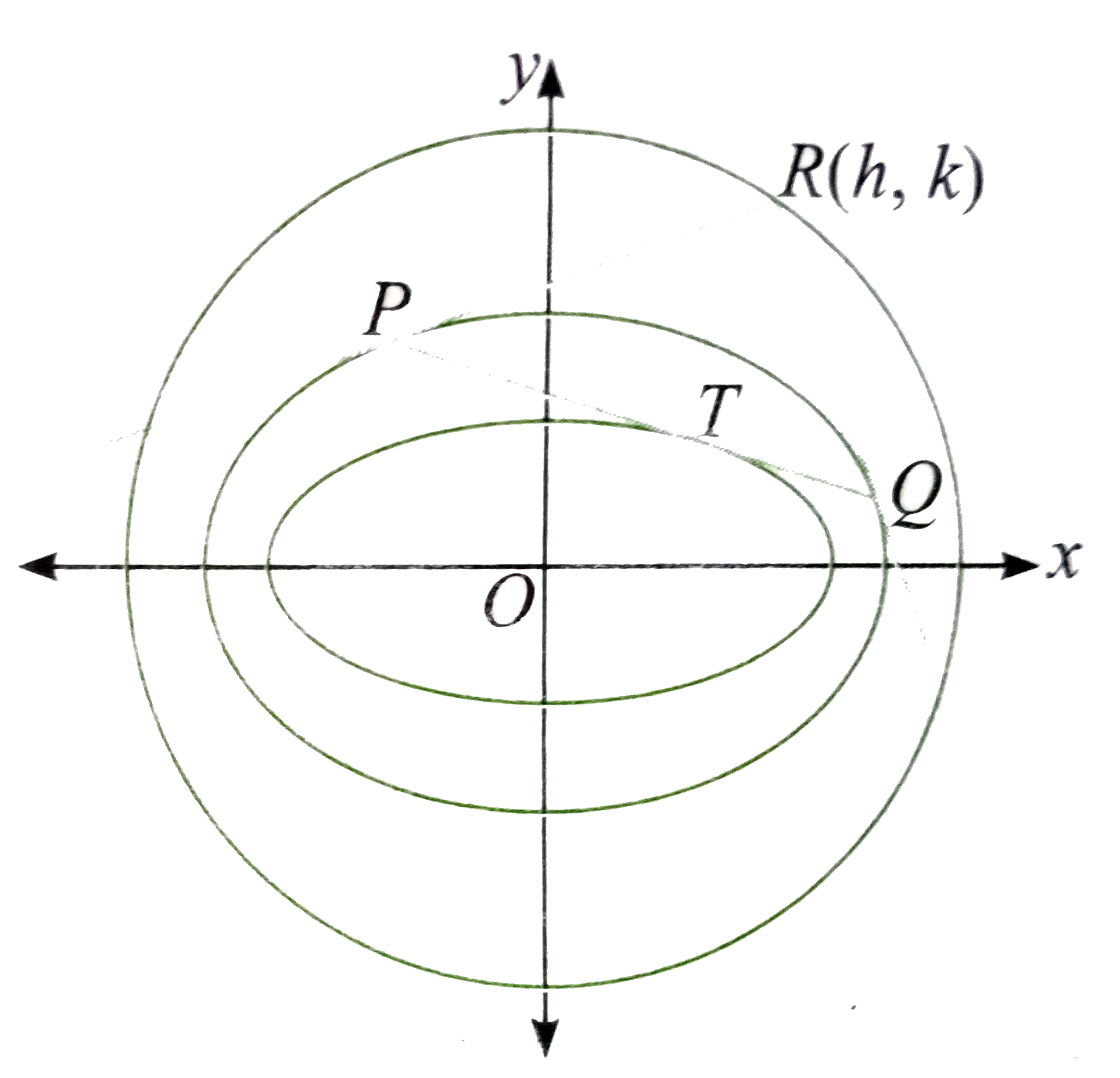
Then the equation of tangent to (1) at point T(2cosθ,sinθ) is given by
xcosθ2+ysinθ1=1 (3)
Let this tangent meet the ellipse (2)at P and Q . Let the tangents drawn to ellipse (2)at P and Q meet each other at R(h,k) .
Tehn PQ is the chord of contact of ellipse (2) with respect to teh point (R(h,k) and is given by
xh6+yk3=1
Clearly, (3) and (4) represent the same line and, hence should be identical.
Therefore, comapring the ratio of coefficients , we get
(cosθ)/2h/6=sinθk/3=11
or h=3cosθ,k=3sinθ
or h2+k2=9
Therfore, hte locus of (h,k) is x2+y2=9
Which is the director circle of he ellipse x26+y23=1
and we know that the director circle is the locus of the point of intersection of the tangents which are at right angle.
Thus, tangents at P and Q are perpendicular
Similar Questions
A tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P and Q. The angle between the tangents at P and Q of the ellipse x2+2y2=6 is
View SolutionA tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P&Q.
View SolutionEllipse x^2 +4y^2 =4 One touch line ellipse x^2+2y^2= 6 Meets at P and Q. Prove that ellipse x^2+y^2 = 6 The tangent lines drawn at P and Q are at right angles.
View Solutionदीर्घवृत्त x2+2y2=6 की किसी जीवा के सिरों पर खींची गयी स्पर्श रेखाओ के प्रतिच्छेदी बिंदु का बिन्दुपथ ज्ञात कीजिये जबकि यह जीवा दीर्घवृत x2+4y2=4 को स्पर्श करती है-
View Solutionदीर्घवृत्त x2+4y2=4 की स्पर्श रेखा, दीर्घवृत्त x2+2y2=6 को P तथा Q पर मिलती है। सिद्ध कीजिए कि P तथा Q पर दीर्घवृत्त x2+2y2=6 की स्पर्श रेखायें समकोण पर होंगी।
View Solutionदीर्घवृत्त x2+4y2=4 की स्पर्श रेखा, दीर्घवृत्त x2+2y2=6 को P व Q बिन्दुओं पर मिलती है। सिद्ध कीजिए कि P व Q पर दीर्घवृत्त x2+2y2=6 की स्पर्श रेखायें लम्बवत् होंगी।
View SolutionA tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P&Q. The angle between the tangents at P and Q of the ellipse x 2 +2y 2 =6 is
View SolutionThe locus of the point of intersection of the tangents at the extremities of the chords of the ellipse x2+2y2=6 which touch the ellipse x2+4y2=4, is x2+y2=4 (b) x2+y2=6 x2+y2=9 (d) None of these
View Solution
