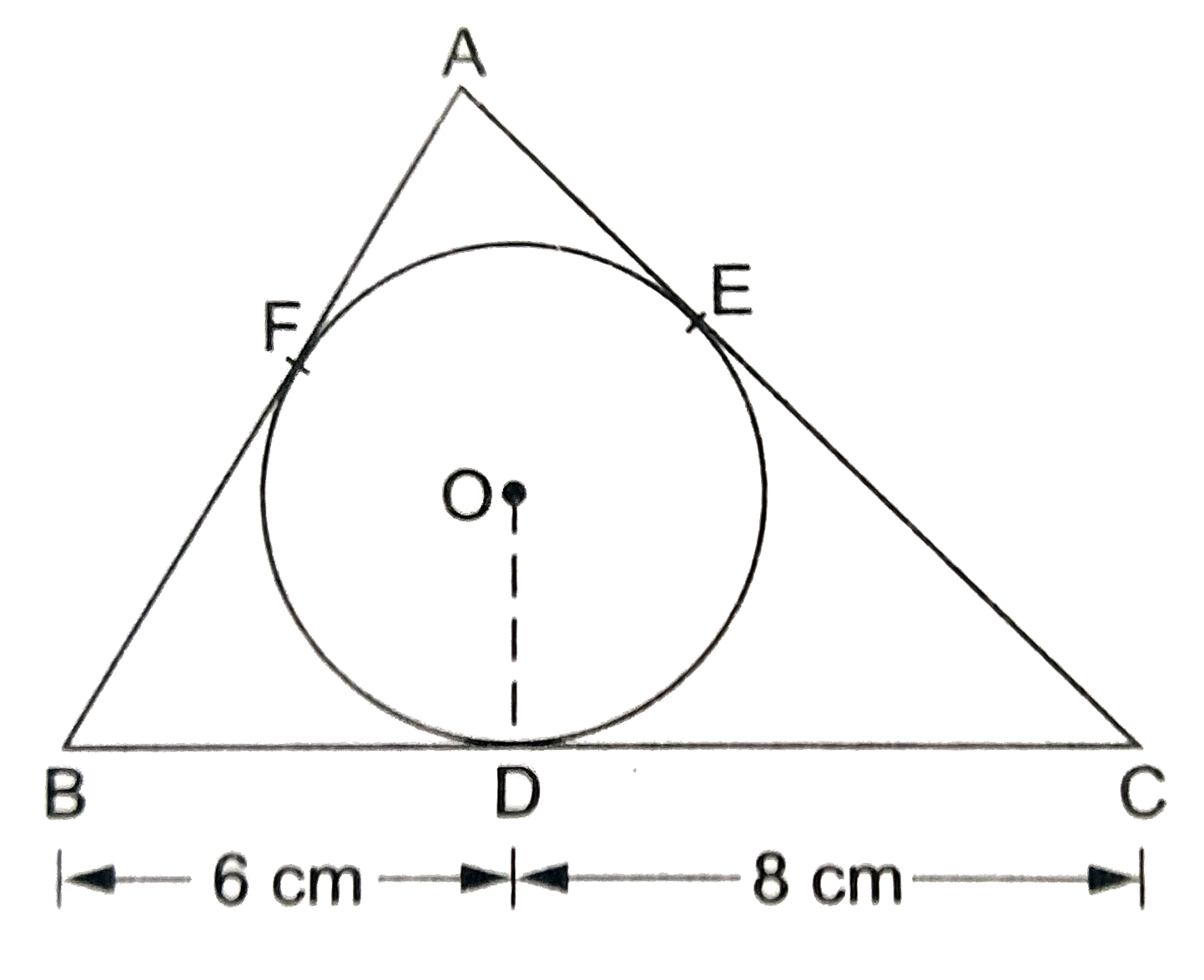
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
Given, CD = 6 cm, BD = 8 cm and radius = 4 cm
Join OC, OA and OB.
We know that the tangents drawn from external point are equal in length
and
Let
In
Area of triangle,
In
Area of triangle, ltbtgt In
Area fo triangle,
Now, semiperimeters of triangle ltvrgt
Now, area of
Using Heron's formula,
Area of
From Eqs. (1) and (2), we get
On squaring both sides,
Length
Length of

Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise25videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question7videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions3videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions9videos
CO-ORDINATE GEOMETRY
Similar Questions
A triangle ABC is drawn to circumscribe a circle of radius 4cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6cm and 8cm respectively. Find the lengths of the sides AB and AC.
 View Solution
View SolutionIn the given figure ΔABC is drawn to circumscribe a circle of radius 3 cm, such that the segment BD and DC into which BC is divided by the point of contact D are of length 6 cm and 8 cm respectively, find side AB if the ar (ΔABC)=63cm2
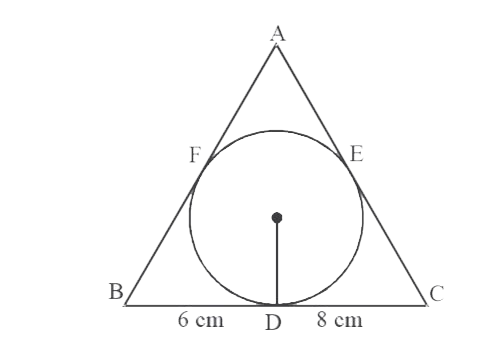 View Solution
View SolutionQ25. Infig.,a triangle ABC is drawn to a circle of radius 3 cm, such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8cm respect Find the side AB if the area of ΔABC=63cm2
View SolutionIn Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR=189cm2, then find the lengths of sides PQ and PR.
View SolutionIn the given figure, a triangle PQR is drawn to circumscribe a circle of radius √3cm such that segments RS and QS into which QR is divided by the point of contact S are of lengths 5cm and 3cm respectively. If the area of ΔPQR is 10√3cm2, then find the sides PQ and PR.
View SolutionIn the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BD and DC are of lengths 6 cm and 9 cm respectively. If the area of △ABC=54cm2, then find the lengths of sides AB and AC. ltBRgt
 View Solution
View SolutionIn Figure, A ABC is drawn to circumscribe a circle of radius 4cm such that the segments BDandDC are of lengths 8cm and 6cm respectively. Find the lengths of sides ABandAC, when area of ABC is 84cm2.
View SolutionA triangle ABC is drawn to circumscribe a circle. If AB = 13 cm, BC = 14 cm and AE =7 cm, then find AC.
 View Solution
View SolutionIn figure , a triangle ABC is drawn to circumscribe a circle of radius 3 cm , such that segments BD and DC are of length 6 cm and 9 cm .If the area of △ABC=54cm2, then find the lengths of the side AB and AC.
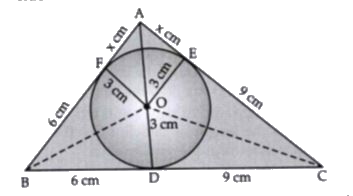 View Solution
View SolutionThe radius of the incircle of a triangle is 4 cm and the segments into which one side is divided by the point of contact are 6 cm and 8 cm. Determine the other two sides of the triangle.
View Solution

