A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced. The table shows the results of 1000 cases.
To solve the problem, we need to determine the probability that a tire from the company will need to be replaced before it has covered a distance of 4000 kilometers.
1. Understand the Data:
The company has recorded the distances covered by tires before they need to be replaced. The frequency of tires needing replacement is given in the following ranges:
- Less than 4000 km: 20 tires
- 4000 to 9000 km: 210 tires
- 9001 to 14000 km: 325 tires
- More than 14000 km: 445 tires
2. Total Cases:
The total number of cases recorded is 1000.
3. Identify Favorable Outcomes:
We are interested in the tires that need to be replaced before covering 4000 km. According to the data, this is represented by the frequency of 20 tires.
4. Calculate Probability:
The probability (P) is calculated using the formula:
P(replaced before 4000 km)=Number of favorable outcomesTotal number of outcomes
Substituting the values:
P(replaced before 4000 km)=201000
5. Simplify the Probability:
Simplifying the fraction:
P(replaced before 4000 km)=20÷201000÷20=150
6. Final Answer:
Therefore, the probability that a tire will need to be replaced before it has covered a distance of 4000 km is:
150
The company has recorded the distances covered by tires before they need to be replaced. The frequency of tires needing replacement is given in the following ranges:
- Less than 4000 km: 20 tires
- 4000 to 9000 km: 210 tires
- 9001 to 14000 km: 325 tires
- More than 14000 km: 445 tires
The total number of cases recorded is 1000.
We are interested in the tires that need to be replaced before covering 4000 km. According to the data, this is represented by the frequency of 20 tires.
The probability (P) is calculated using the formula:
P(replaced before 4000 km)=Number of favorable outcomesTotal number of outcomes
Substituting the values:
P(replaced before 4000 km)=201000
Simplifying the fraction:
P(replaced before 4000 km)=20÷201000÷20=150
Therefore, the probability that a tire will need to be replaced before it has covered a distance of 4000 km is:
150
Topper's Solved these Questions
Similar Questions
A tyre manufacturing company kept a record of the distance covered before a tyre to be replaced. Following table shows the results of 1000 cases. Distance in km: Less tan 400 400 to 900 900 to 1400 More than 1400 Number of tyres: 210 325 385 80 If you buy a tyre of this company, what is the probability that: (i) it will need to be replaced before it has covered 400 km? (ii) it will last more than 900 km? (iii) it will need to be replaced after it has covered somewhere between 400 km and 1400 km? (iv) it will not need to be replaced at all? (v) it will need to be replaced?
View SolutionA tyre manufacturing company kept a record of the distance covered before a tyre to be replaced. Following table shows the results of 1000 cases. Distance ∈ km: Less than 400 400 → 900 900 → 1400 More than 1400 N⊙ of tyres: 210 325 385 80 If you buy a tyre of this company, what is the probability that: it will need to be replaced before it has covered 400 km? it will last more than 900 km? it will need to be replaced after it has covered somewhere between 400km and 1400 km? it will not need to be replaced at all it will need to be replaced?
View Solution
Knowledge Check
- Question 1 - Select One
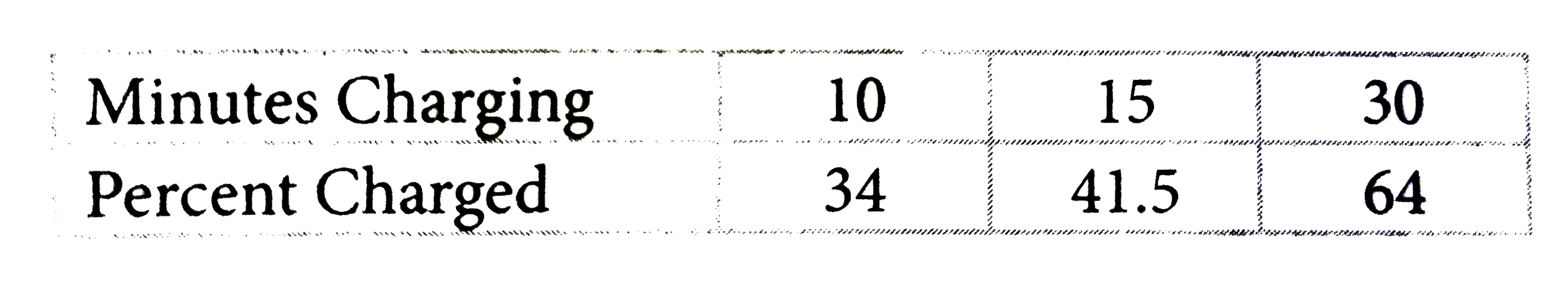
Xia is charging her laptop. She records the battery charge for the first 30 minutes after she plugs it in to get an idea of when it will be completely charged. The table above shows the results. If y is the percent battery charge on Xia's laptop, which linear equation represents the correct relationship between y and x ?Ay=1.5x+19By=2x+14Cy=2.5x+9Dy=10x+34 - Question 2 - Select One
Read the passage given and answer the questions that follow:
On 31 January 1930, Mahatma Gandhi sent a letter to Viceroy Irwin stating and imposing eleven demands. Among all the demands, the most stirring of all the demands was to abolish the salt tax that is consumed by the rich and the poor. The demands were needed to be fulfilled by 11 March or else the Congress will initiate a civil disobedience campaign. The popular salt march was started by Mahatma Gandhi and it was accompanied by 78 of his trusted volunteers. The march covered over 240 miles, from Gandhi's ashram in a place called Sabarmati to the Gujarati coastal town of Dandi. On 6 April he reached Dandi, and ceremonially violated the law, and started manufacturing salt by boiling seawater. This movement marked the beginning of the Civil Disobedience Movement
How much distance covered by M. K. Gandhi during Dandi March?A200 MilesB240 MilesC250 MilesD260 Miles
A vehicle of mass 500 kg is moving with a velocity of 15ms−1. It is brought to rest by a retarding force. Find the distance moved by the vehicle before coming to rest, if the sliding friction between the tyres and the road is 3000N.
View SolutionThe coefficient of friction between the tyres and road is 0.4. The minimum distance covered before attaining a speed of 8ms−1 starting from rest is nearly ( take g=10ms−2)
View SolutionWe wish to obtain an equal sized inverted image of a candle flame on a screen kept at a distance of 4 m from the candle flame.
(a) Name the type of lens that should be used.
(b) what should be the focal length of the lens and at what distance from the candle flame the lens be placed ?
(c) Draw a labelled diagram to show the image formation in this case.View SolutionAs mosquito is sitting on an L.P. record disc rotating on a trun tabel at 3313 revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π281. Take g=10ms2
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
Based on this data, the best guess for the value of n is :-View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
The student performs another trial in which the ball is launched at speed 5.0m/s. Its range is approximately:View Solution

