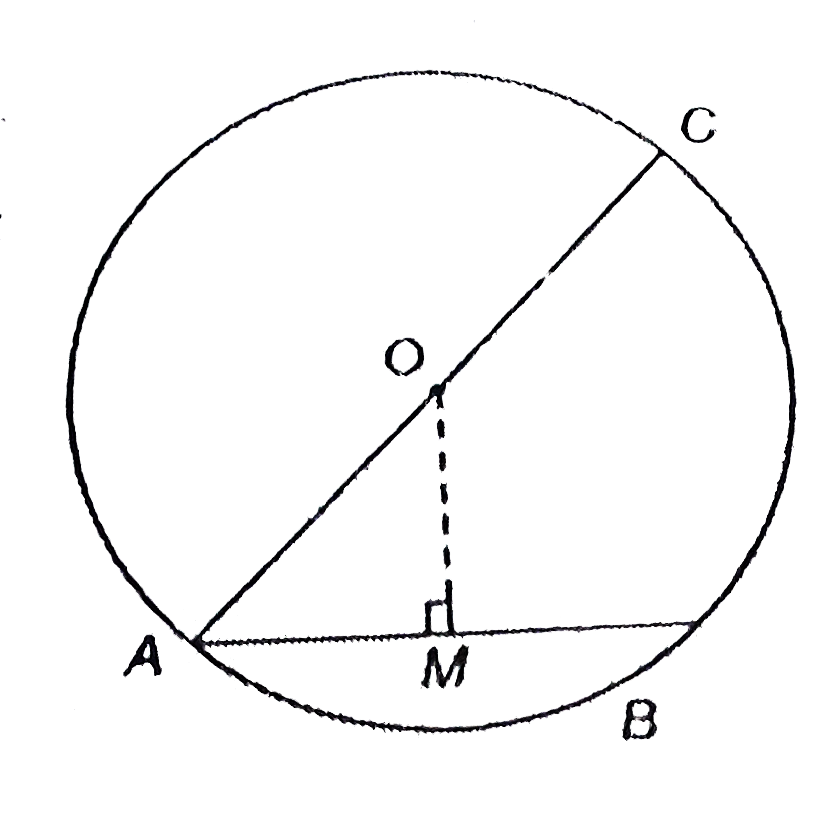
AB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
Step by step video solution for AB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q^(2)=p^(2)+3r^(2). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
There is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
A4.8 cmB10.8cmC9.6 cmDnone of these
In a circle of radius 5 cm, AB and Ac are two chords of 6cm each. Find the length of the chord BC.
View SolutionIn a circle of radius 8 cm, AB and AC are two chords such that AB = AC = 12 cm. What is the length of chord BC ?
View SolutionIn a rhombus ABCD, prove that AC2+BD2=4AB2
View SolutionFor a rhambus ABCD , prove that 4AB2=AC2+BD2
View SolutionIn a circle of radius 5cm, AB and AC are two chords such that AB=AC=8 cm. What is the length of chord BC?
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
 View Solution
View Solution

