AB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
Video Solution
Text Solution
Given In a circle of radius r, there are two chords AB and AC such that AB= 2AC. Also, the distance of AB and AC from the centre are p and q, respectively.
To prove 4q2=p2+3r2,
Proof Let AC=a, then AB = 2a
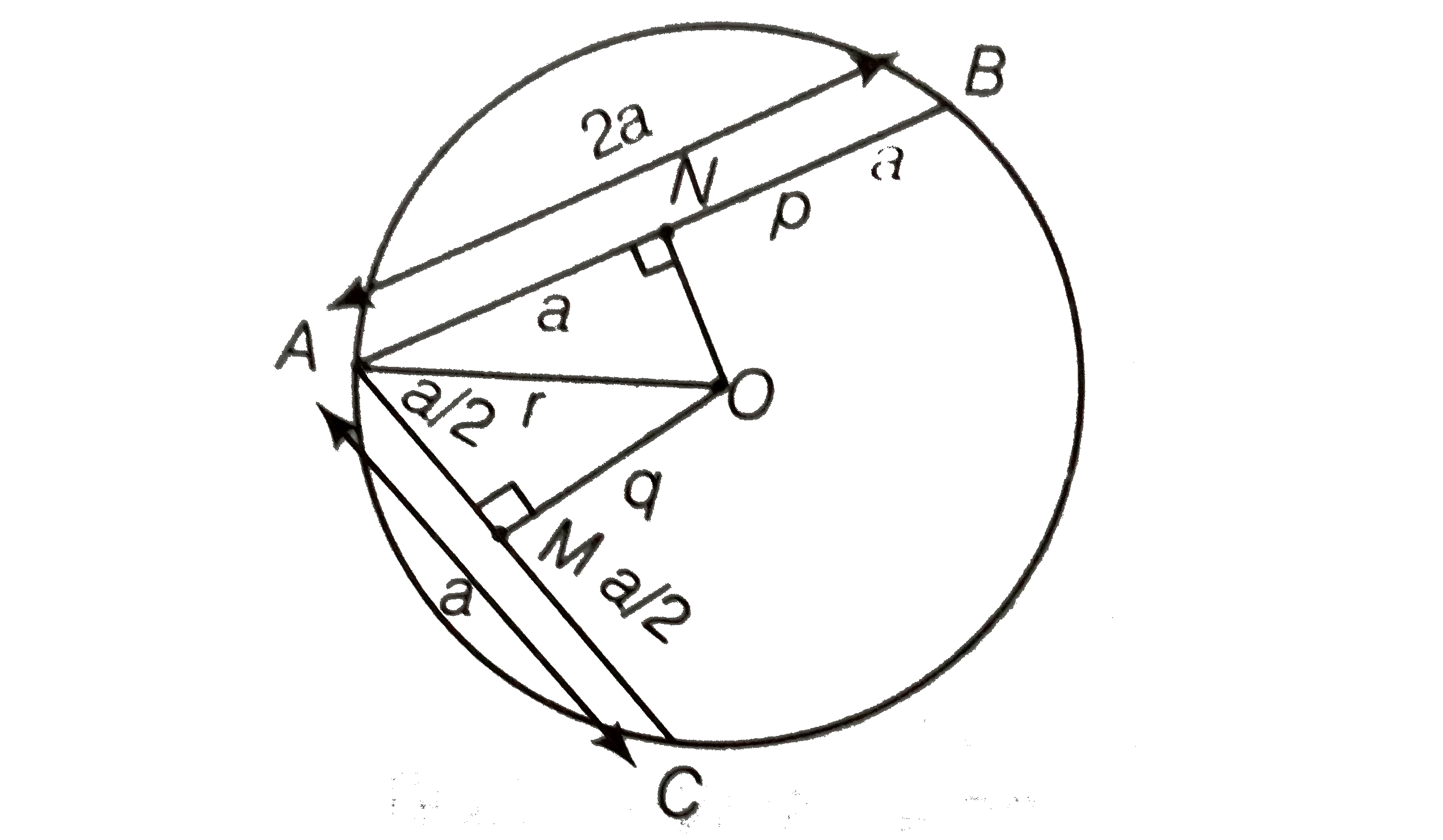
From centre O, perpendicular is drawn to the chords AC and AB at M and N, respectively.
∴AM=MC=a2
AN=NB=a
In ΔOAMAO2=AM2+MO2 [by Pythagoras theorem]
⇒AO2=(a2)2+q2 ....(i)
In ΔOAN, use Pythagoras theorem,
AO2=(AN)2+(NO)2
⇒AO2=(a)2+p2 ...(ii)
From Eqs. (i) and (ii),
(a2)2+q2=a2+p2
⇒a24+q2=a2+p2
⇒a2+4q2□=4a2+4p2 [multiplying both sides by 4]
⇒4q2=3a2+4p2
⇒4q2=p2+3(a2+p2)
⇒4q2=p2+3r2[In right angled ΔOAN,r2=a2+p2]
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
There is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
A4.8 cmB10.8cmC9.6 cmDnone of these
In a circle of radius 5 cm, AB and Ac are two chords of 6cm each. Find the length of the chord BC.
View SolutionIn a circle of radius 8 cm, AB and AC are two chords such that AB = AC = 12 cm. What is the length of chord BC ?
View SolutionFor a rhambus ABCD , prove that 4AB2=AC2+BD2
View SolutionIn a rhombus ABCD, prove that AC2+BD2=4AB2
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View SolutionIn a circle of radius 5cm, AB and AC are two chords such that AB=AC=8 cm. What is the length of chord BC?
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
View Solution
