AB and CD are chords of a circle with centre O. AB = 48 cm and its distance from centre O is 10 cm. If the distance of CD from centre O is 24 cm, find the length of CD.
The correct Answer is:20 cm
To solve the problem, we will follow these steps:
Step 1: Understand the given information
We have two chords AB and CD in a circle with center O. The length of chord AB is given as 48 cm, and its distance from the center O is 10 cm. The distance of chord CD from the center O is 24 cm. We need to find the length of chord CD.
Step 2: Find the half-length of chord AB
Since the distance from the center O to chord AB is 10 cm, we can denote the midpoint of AB as M. The property of a chord states that the line from the center to the chord is the perpendicular bisector. Therefore, we can find the half-length of AB.
AM=MB=AB2=48 cm2=24 cm
Step 3: Apply the Pythagorean theorem to triangle OMB
In triangle OMB, we can apply the Pythagorean theorem. Here, OM is the distance from the center to the chord (10 cm), and MB is half the length of the chord (24 cm). We need to find the radius OB.
Using the Pythagorean theorem:
OB2=OM2+MB2
Substituting the values:
OB2=102+242
OB2=100+576=676
OB=√676=26 cm
Step 4: Set up for chord CD
Let the length of chord CD be denoted as 2x. The midpoint of CD is N, and the distance from the center O to chord CD is 24 cm (ON).
Step 5: Apply the Pythagorean theorem to triangle ODN
In triangle ODN, we apply the Pythagorean theorem again:
OD2=ON2+DN2
Substituting the known values:
OB2=ON2+DN2
262=242+x2
676=576+x2
x2=676−576=100
x=√100=10 cm
Step 6: Find the length of chord CD
Since CD = 2x, we have:
CD=2×10=20 cm
Final Answer
The length of chord CD is 20 cm.
---
We have two chords AB and CD in a circle with center O. The length of chord AB is given as 48 cm, and its distance from the center O is 10 cm. The distance of chord CD from the center O is 24 cm. We need to find the length of chord CD.
Since the distance from the center O to chord AB is 10 cm, we can denote the midpoint of AB as M. The property of a chord states that the line from the center to the chord is the perpendicular bisector. Therefore, we can find the half-length of AB.
In triangle OMB, we can apply the Pythagorean theorem. Here, OM is the distance from the center to the chord (10 cm), and MB is half the length of the chord (24 cm). We need to find the radius OB.
OB2=100+576=676
OB=√676=26 cm
Let the length of chord CD be denoted as 2x. The midpoint of CD is N, and the distance from the center O to chord CD is 24 cm (ON).
In triangle ODN, we apply the Pythagorean theorem again:
262=242+x2
676=576+x2
x2=676−576=100
x=√100=10 cm
Since CD = 2x, we have:
The length of chord CD is 20 cm.
Topper's Solved these Questions
- CIRCLES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTIONS (MCQ.s)
14 Videos
- CIRCLES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SUM TO ENRICH REMAMBER
6 Videos
- CIRCLES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - EXERCISE 10.6
10 Videos
- INTRODUCTION TO EUCLID.S GEOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
3 Videos
Similar Questions
Radius of circle is 34 cm. And distance of chord from centre is 24 cm. Find length of the chord?
View SolutionAB is a chord of circle with centre O. At B, a tangent PB is drawn such that its length is 24 cm. The distance of P from the centre is 26 cm. If the chord AB is 16 cm, find its distance from the centre.
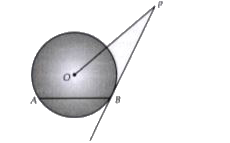
View Solution
Knowledge Check
Length of a chord PQ of a circle with centre O is 4 cm. If the distance of PQ from the centre of circle is 2 cm, then the length of the diameter is:
A2√2cm.B3√2cm.C5√2cm.D4√2cm.The length of the radius of a circle with centre O is 5 cm and the length of the chord AB is 8 cm. The distance of the chord AB from the point O is
A2 cm.B3 cm.C4 cm.D15 cm.
AB is a chord of a circle with centre O and diameter 20 cm. If AB = 12 cm, find the distance of AB from O.
View SolutionA chord AB is drawn in a circle with centre O and radius 5 cm. If the shortest distance between centre and chord is 4 cm, find the length of chord AB?
View SolutionB is a tangent to the circle with centre O to B. AB is a chord of length 24 cm at a distance of 5 cm from the centre. If the tangent is of length 20 cm, find the length of PO.
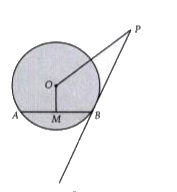
View SolutionAB and CD are equal and parallel chords of a circle with centre O. Then AC passes through the centre O. [Agree / Disagree]
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=50∘ then find ∠AOC
View SolutionAB and CD are 2 chords of circle such that AB = 8 cm, CD = 10 cm distance b/w chord is 2 cm . If chords are on same side find radius
View Solution
