AB and CD are two parallel chords of a circle on opposite sides of a diameter such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords.
To solve the problem, we need to find the distance between the two parallel chords AB and CD in a circle with a radius of 13 cm. The lengths of the chords are given as AB = 24 cm and CD = 10 cm.
1. Draw the Circle and Chords:
- Draw a circle with center O and radius 13 cm.
- Draw two parallel chords AB and CD on opposite sides of the diameter.
2. Identify the Midpoints of the Chords:
- Since AB = 24 cm, the midpoint E of chord AB divides it into two equal parts, AE = 12 cm.
- Since CD = 10 cm, the midpoint F of chord CD divides it into two equal parts, CF = 5 cm.
3. Apply the Pythagorean Theorem:
- For chord AB:
- In triangle AOE (where O is the center, A is one endpoint of the chord, and E is the midpoint), we can apply the Pythagorean theorem:
OA2=OE2+AE2
- Here, OA = 13 cm (radius), AE = 12 cm, and OE is the distance from the center O to the chord AB (denote it as D1).
132=D12+122
169=D12+144
D12=169−144=25
D1=√25=5 cm
4. Repeat for Chord CD:
- For chord CD:
- In triangle COF (where O is the center, C is one endpoint of the chord, and F is the midpoint), we apply the Pythagorean theorem:
OC2=OF2+CF2
- Here, OC = 13 cm (radius), CF = 5 cm, and OF is the distance from the center O to the chord CD (denote it as D2).
132=D22+52
169=D22+25
D22=169−25=144
D2=√144=12 cm
5. Calculate the Distance Between the Chords:
- The distance between the two chords is the sum of D1 and D2:
Distance=D1+D2=5 cm+12 cm=17 cm
Final Answer:
The distance between the two chords AB and CD is 17 cm.
- Draw a circle with center O and radius 13 cm.
- Draw two parallel chords AB and CD on opposite sides of the diameter.
- Since AB = 24 cm, the midpoint E of chord AB divides it into two equal parts, AE = 12 cm.
- Since CD = 10 cm, the midpoint F of chord CD divides it into two equal parts, CF = 5 cm.
- For chord AB:
- In triangle AOE (where O is the center, A is one endpoint of the chord, and E is the midpoint), we can apply the Pythagorean theorem:
OA2=OE2+AE2
- Here, OA = 13 cm (radius), AE = 12 cm, and OE is the distance from the center O to the chord AB (denote it as D1).
132=D12+122
169=D12+144
D12=169−144=25
D1=√25=5 cm
- For chord CD:
- In triangle COF (where O is the center, C is one endpoint of the chord, and F is the midpoint), we apply the Pythagorean theorem:
OC2=OF2+CF2
- Here, OC = 13 cm (radius), CF = 5 cm, and OF is the distance from the center O to the chord CD (denote it as D2).
132=D22+52
169=D22+25
D22=169−25=144
D2=√144=12 cm
- The distance between the two chords is the sum of D1 and D2:
Distance=D1+D2=5 cm+12 cm=17 cm
The distance between the two chords AB and CD is 17 cm.
Topper's Solved these Questions
- MATHEMATICS -2017BOOK - ICSECHAPTER - MATHEMATICS -2017EXERCISE - SECTION - B
1 Videos
- MATHEMATICS -2017BOOK - ICSECHAPTER - MATHEMATICS -2017EXERCISE - SECTION- B
30 Videos
- MATHEMATICS -2016BOOK - ICSECHAPTER - MATHEMATICS -2016EXERCISE - SECTION- B
30 Videos
- MATHEMATICS- 2015BOOK - ICSECHAPTER - MATHEMATICS- 2015EXERCISE - SECTION- B
36 Videos
Similar Questions
AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10cm, CD=24cm and the distance between AB and CD is 17cm. Find the radius of the circle.
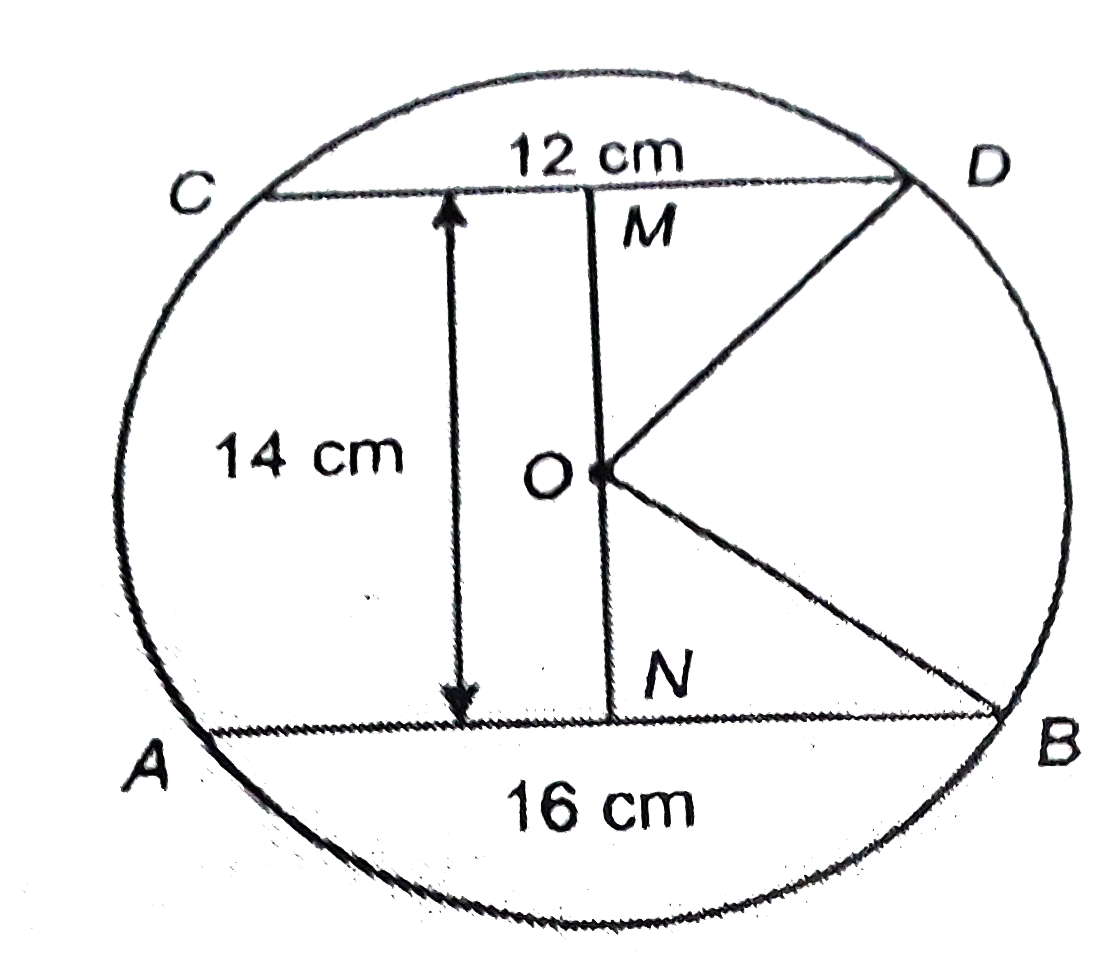
View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
View SolutionAB and CD are two chords of a circle intersecting at a point P inside the circle. If
AB= 24cm, AP= 4cm and PD = 8cm, determine CP
View SolutionChords AB and CD of a circle are parallel to each other and lie on opposite sides of the centre of the circle. If AB = 36 cm, CD = 48 cm and the distance between the chords is 42 cm, find the radius of the circle.
View SolutionThe length of two parallel chords of a circle are 6 cm and 8 cm . The radius of the circle is 5 cm. Find the distance btween them if :
(i) chords are on the same side of the centre.
(ii) chords are on the opposite side of the centre.
View SolutionIn a circle of radious 17 cm, two parallel chords are drawn on opposite side of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is (a) 34 cm (b) 15 cm (c) 23 cm (d) 30 cm
View SolutionIn the given diagram 'O is the centre of the circle and AB is parallel to CD. AB = 24 cm and distance between he chord AB and CD is 17 cm. It the radius of the circle is 13 cm, find the length of the chord CD.
View SolutionAB and CD are two chords of a circle intersecting at a point P inside the circle. If
AP=3cm, PB= 2.5cm and CD= 6.5 cm, determine CP.
View SolutionTwo parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm, find the length of the other chord.
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.
View Solution
