AB is a chord of the circle x2+y2=252 .P is a point such that PA = 4, PB = 3. If AB = 5, then distance of P from origin can be:
9√2
3√2
5√2
7√2 or 1√2
The correct Answer is:D

OA=OB= radius =5√2 and AB=5
⇒∠AOB=π2⇒∠OAB=45∘
Again PA=4,PB=3 and AB=5⇒∠BPA=90∘
Let ∠PAB=θ.
Then OP2=OA2+AP2−2.OA.APcos(45∘±θ)
=252+16−25√241√2(cosθ±sinθ)
=572−20(45±35)=492 or 12
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
A variable line through A(6, 8) meets the circle x2+y2=2 at B and C. P is a point on BC such that AB, AP, AC are in H.P. Then the minimum distance of the origin from locus of P is
View SolutionAB is a chord of circle with centre O. At B, a tangent PB is drawn such that its length is 24 cm. The distance of P from the centre is 26 cm. If the chord AB is 16 cm, find its distance from the centre.
View Solution
Knowledge Check
AB is a chord of the circle x2+y2=25. The tangents of A and B intersect at C. If (2, 3) is the mid-point of AB,then area of the quadrilateral OACB is
A50√133B50√313C50√3D50√3
AB is a chord of the circle x2+y2=25. The tangents of A and B intersect at C. If (2, 3) is the mid-point of AB,then area of the quadrilateral OACB is
View SolutionAB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionP(3,2)" is a point on the circle "x2+y2=13" .Two points "A" ,"B" are on the circle such that PA=PB=√5 .The equation of chord "AB" is
View SolutionIn the figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion.
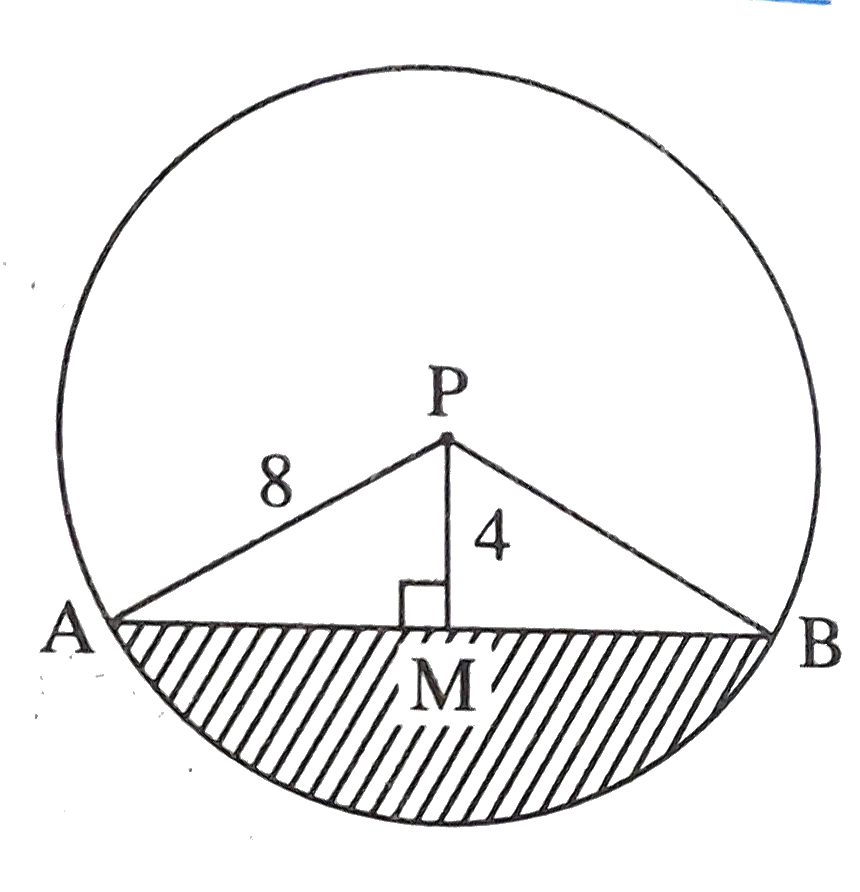
View SolutionTangents are drawn from P(3,0) to the circle x2+y2=1 touches the circle at points A and B. The equation of locus of the point whose distances from the point P and the line AB are equal is
View SolutionFrom the point A(0,3) on the circle x2+4x+(y−3)2=0 a chord AB is drawn to a point such that AM = 2AB. The equation of the locus of M is :-
View SolutionIf the common tangents to the parabola x2=4y and the circle x2+y2=4 intersectat the point P, then the distance of P from the origin, is.
View Solution
