AB is a diameter of a circle with centre O. A line drawn through the point A intersects the circle at the point C and the tangent through B at the point D. Prove that (a)BD2=AD.DC . (b) The area of the rectangle of formed by AC and AD for any straight line is always equal.Solution in Bengali
Step by step video & image solution for AB is a diameter of a circle with centre O. A line drawn through the point A intersects the circle at the point C and the tangent through B at the point D. Prove that (a) BD^(2)=AD.DC . (b) The area of the rectangle of formed by AC and AD for any straight line is always equal. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITYBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMILARITYEXERCISE - Exercise 5.1
32 Videos
- SIMILARITYBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMILARITYEXERCISE - Exercise 5.2
27 Videos
- SAMPLE QUESTIONS PAPERSBOOK - CALCUTTA BOOK HOUSECHAPTER - SAMPLE QUESTIONS PAPERSEXERCISE - QUESTION
157 Videos
- SIMPLE INTERESTBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMPLE INTERESTEXERCISE - Long-answer type questions
37 Videos
Similar Questions
In the following figure , ∠P=
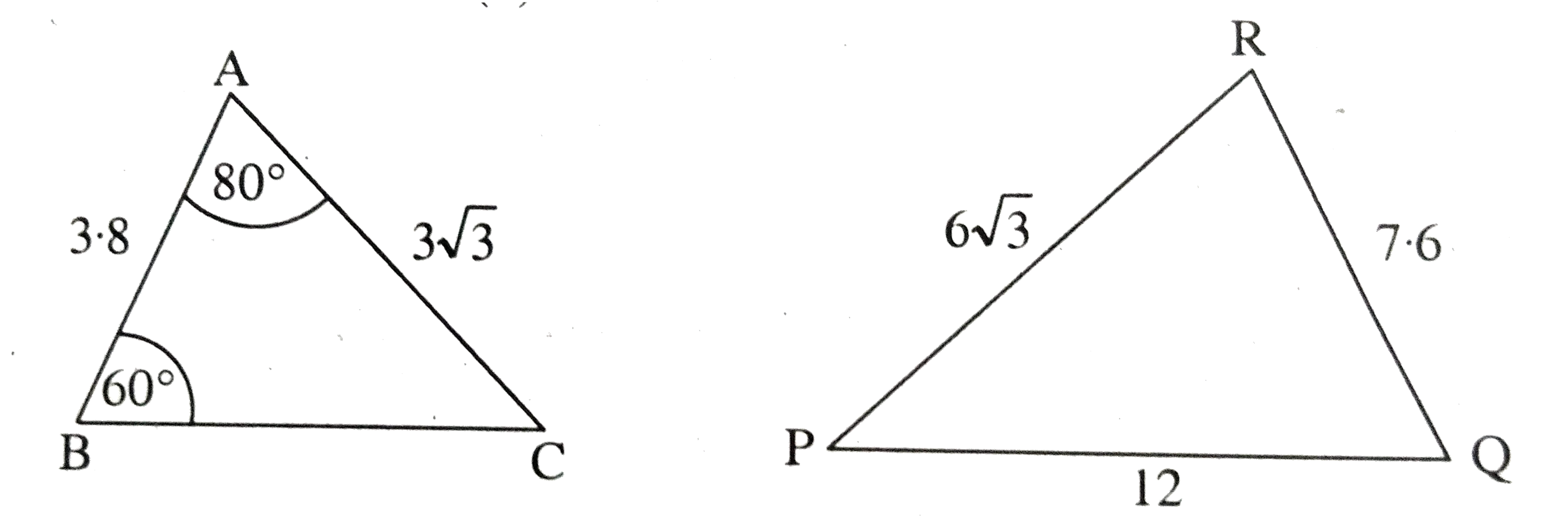
View SolutionIn ΔPQR and ΔDEF, PQDE=QREF=RPFD. Then which one of the following is correct?
View SolutionA person deposite ₹ 100 in a bank and after 2 yars he got a total ₹121 as a return. Then the componund interest of the bank per annum is
View SolutionGoutam took a loan of some money from a cooperative bank for opening a poultry farm at the rate of simple interest of 12% per annum. Every month he has to repay 378Rs as interest. Determine the loan amount taken by him.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
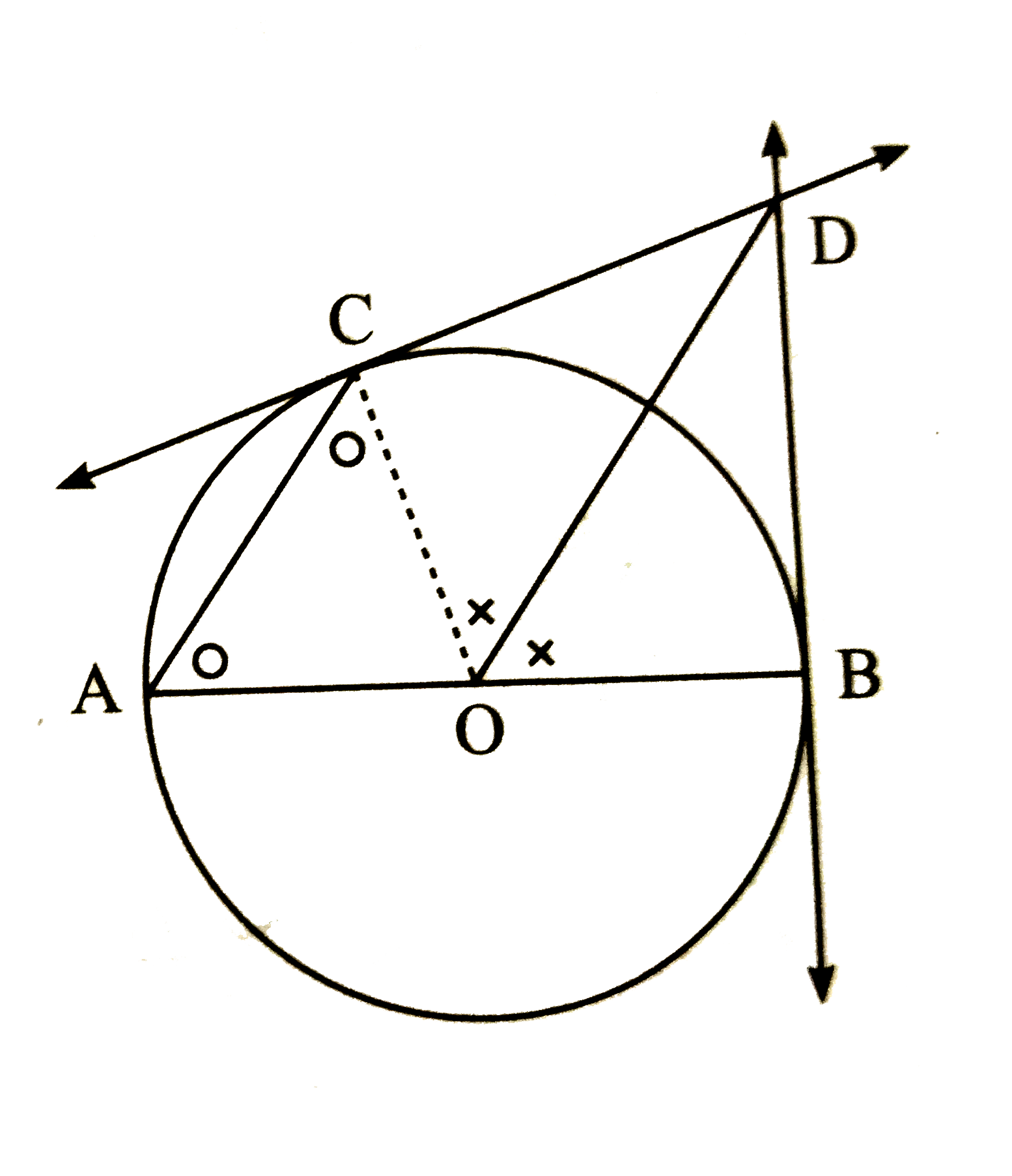
View SolutionThe centre of two circle are P and Q they intersect at the points A and B. The straight line parallel to the line segment PQ through the point A intersects the two circles at the point C and D Prove that CD=2PQ
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
View SolutionIn two circles , one circle passes through the centre O of the other circle and they intersect each other at the points A and B . A straight line passing through A intersect the circle passing through O at the point P and the circle with centre at O at the point R . BY joining P , B and R , B prove that PR= PB.
View SolutionThe straight line PAB intersects the circle with centre O at the points A and B. The straight line PAB will be a tangent to that circle if AB=_______
View SolutionIn the adjoining figure, O is the centre and seg AB is a diameter. At the point C on the circle, the tangent CD is drawn. Line BD is a tangent to the circle at the point B. Show that segOD ∣∣ chord AC.
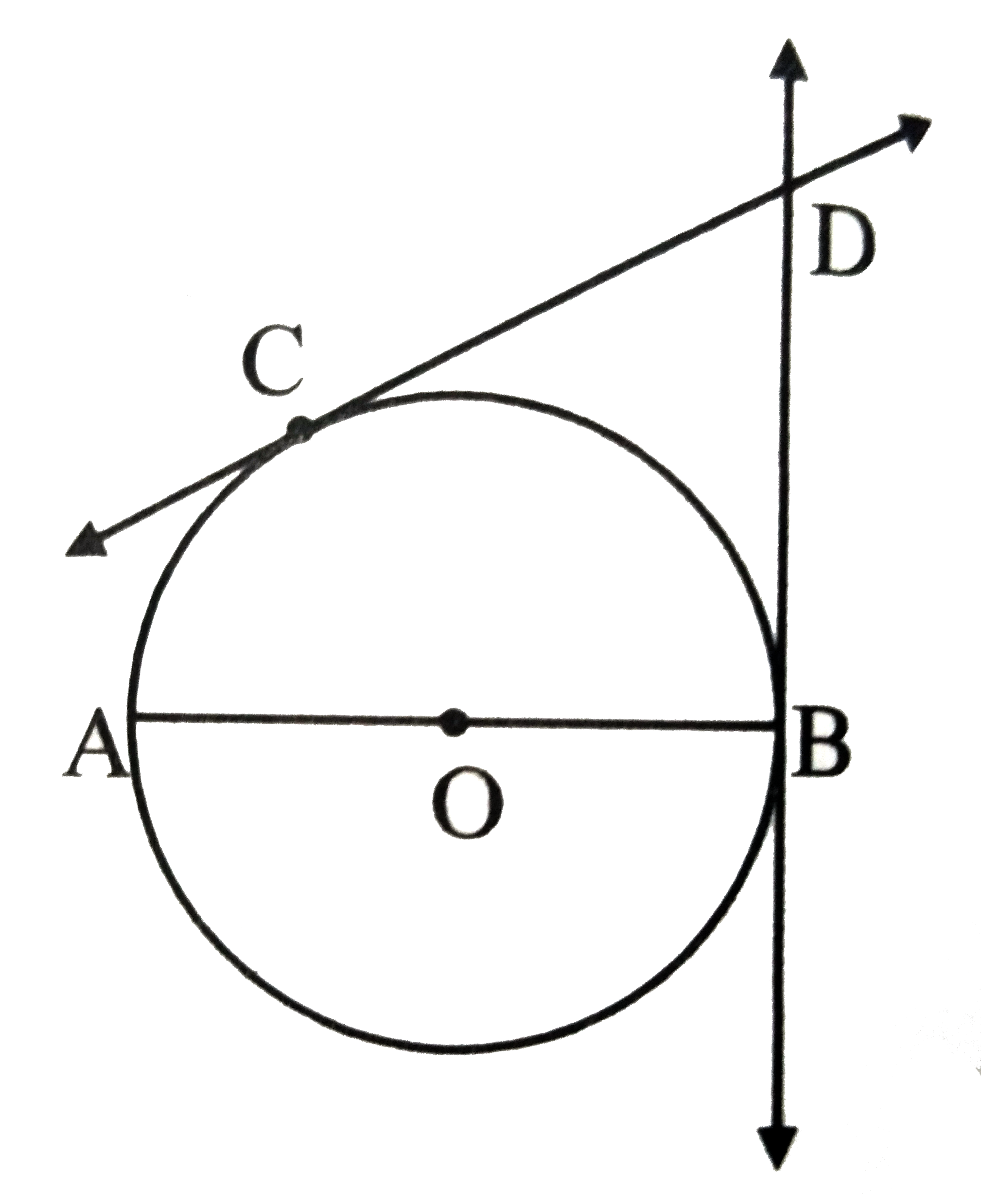
View SolutionAB is a diameter of a circle. BP is a tangent to the circle at B. A straight line passing through A intersects BP at C and the circle at D. Prove that BC2=AC×CD.
View SolutionAB is a diameter of a circle with centre O, P is any point on the circle, the tangent drawn through the point P intersects the two tangents drawn through the points A and B at the points Q and R respectively. If the radius of the circle be r, then prove that PQ.PR=r2.
View SolutionO কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ কর যে, BD^2=AD.DC
View SolutionO কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ কর যে, যে কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান।
View Solution
