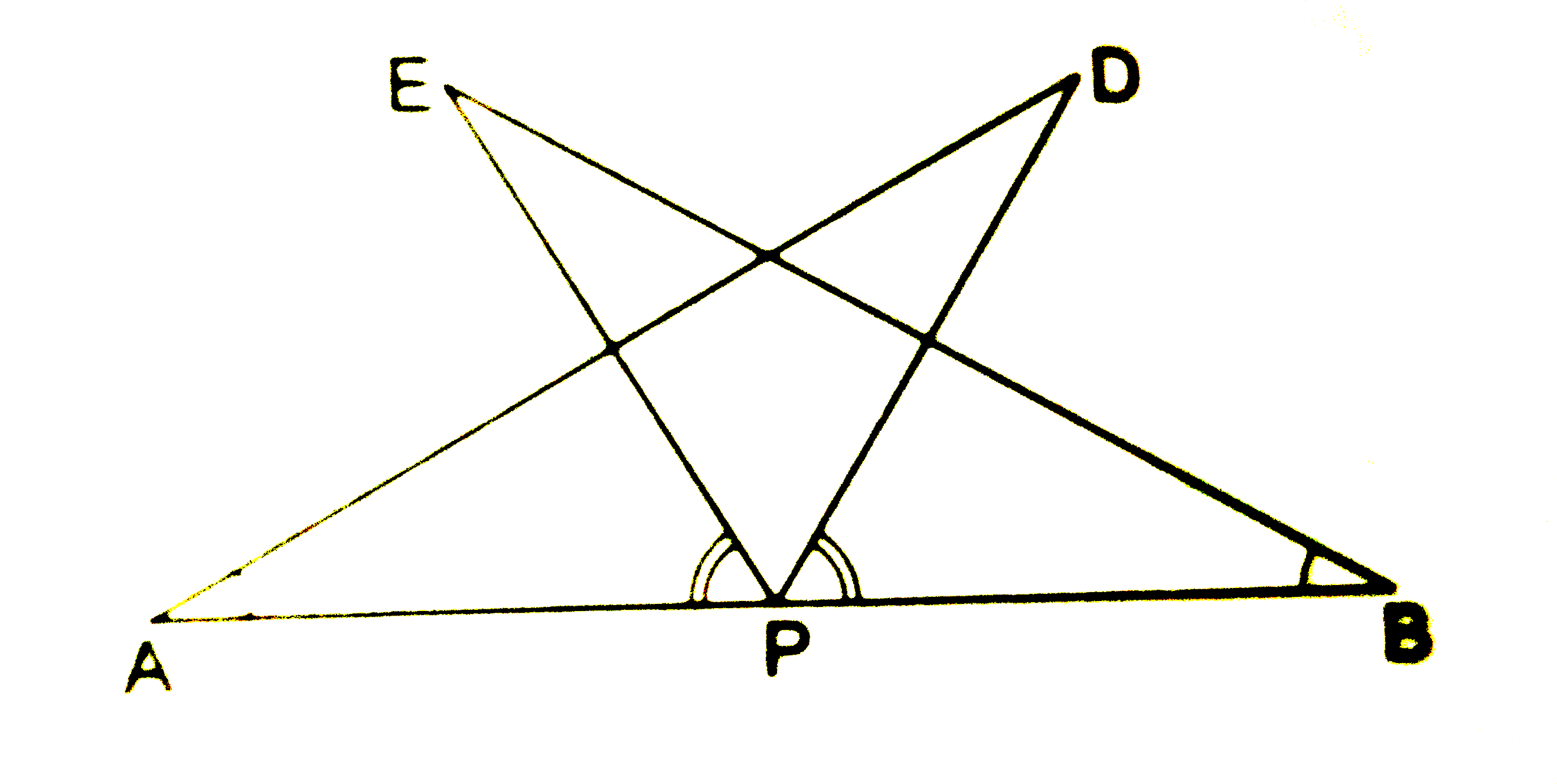
AB is a line segment D and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

ΔDAP≅ΔEBP
Step by step video & image solution for AB is a line segment D and P is its mid-point. D and E are points on the same side of AB such that angleBAD = angleABE and angleEPA = angleDPB (see figure). Show that DeltaDAP~=DeltaEBP by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.2)9videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.3)10videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLES14videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner20videos
STATISTICS
Similar Questions
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

AD=BEView SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If C is the mid-point of AB and P is any point outside AB, then
APA + PB = PCBPA + PB + 2 PC = 0CPA + PB - 2PC = 0DPA + PB + PC = 0 - Question 2 - Select One
If C is the mid-point of AB and P is any point outside AB, then
APA+PB+PC=0BPA+PB+2PC=0CPA+PB=PCDPA+PB=2PC
AB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
AD=BEView SolutionAB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
ΔDAP≡ΔEBPView SolutionIn the given Fig., D and E are points on sides AB and CA of △ABC such that △B=∠AED. Show that △ABC~△AED.
 View Solution
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
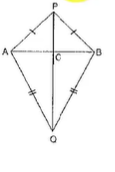 View Solution
View SolutionD is a point on side BC of triangle ABC such that AD = AC (see figure). Show that AB>AD.
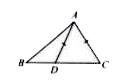 View Solution
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View Solution
