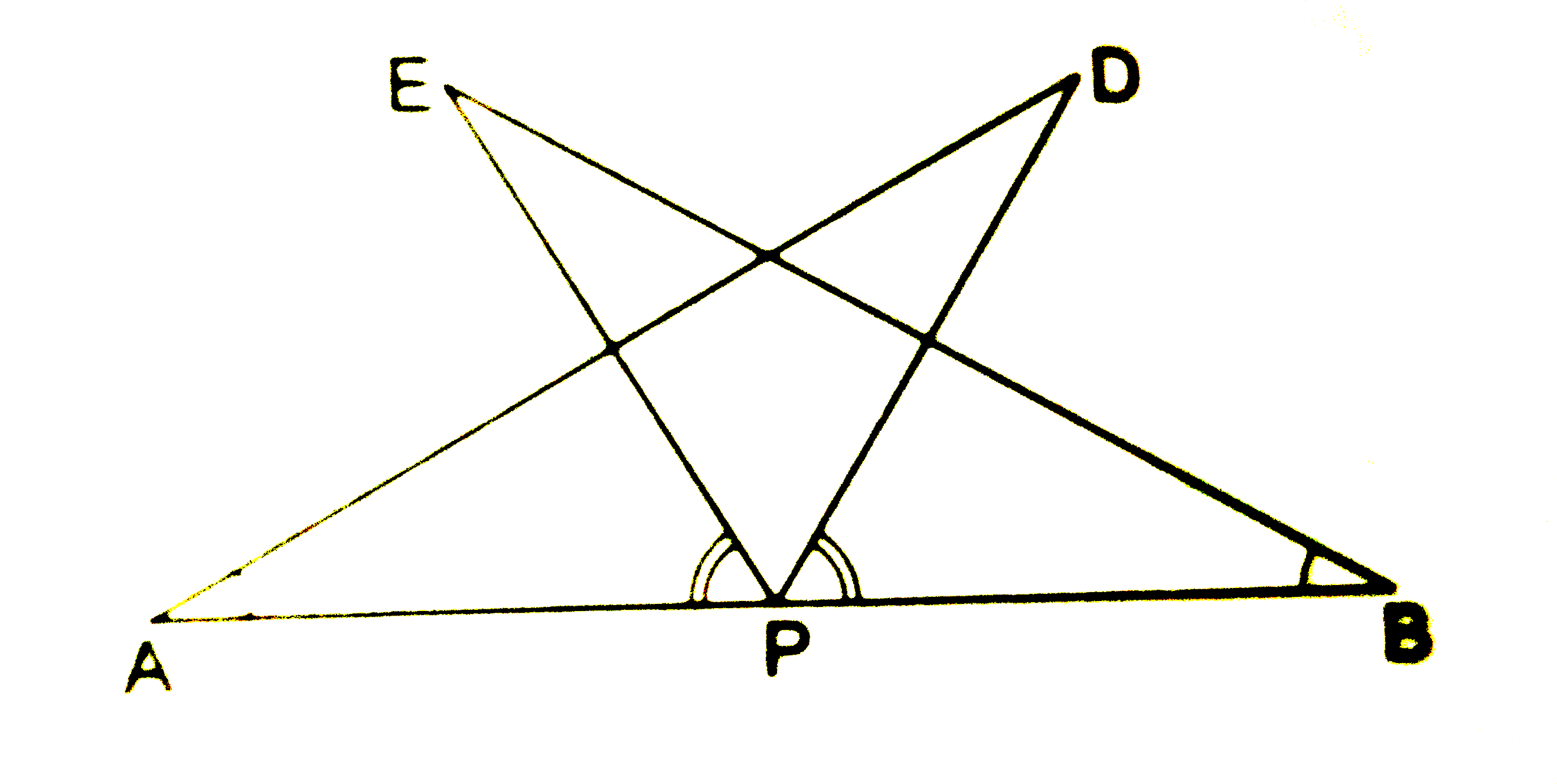
AB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
ΔDAP≡ΔEBP
Step by step video & image solution for AB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that angleBAD=angleABE and angleEPA=angleDPB. Prove that DeltaDAP-=DeltaEBP by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5A47videos
CONGRUENCE AND SIMILAR TRIANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - ELEMENTARY TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE 11B37videos
ELEMENTARY TRIGONOMETRIC IDENTITIES
Similar Questions
AB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
AD=BEView SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A point C is called the midpoint of a line segment ¯¯¯¯¯¯AB if
AC is an intrerior points of ABBAC =CBCC is an interior point of AB such that ¯¯¯¯¯¯AC=¯¯¯¯¯¯CBDAC+CB=AB - Question 2 - Select One
If C and D are the points of internal and external division of line segment AB in the same ratio, then AC,AB, AD are in
AAPBGPCHPDAGP
AB is a line segment D and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

ΔDAP≅ΔEBPView SolutionAB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

AD=BEView SolutionAB is a line segment, AX and BY are two equal line segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P, prove that
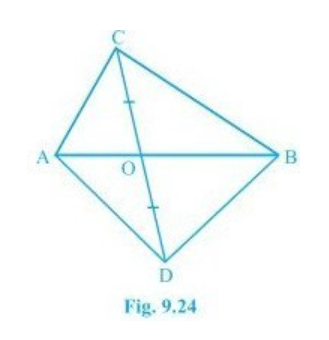
ΔAPX≅ΔBPYView SolutionIn Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(△ABC)=ar(△ABD)
View SolutionAB is a line segment. AX and BY are two equal line segments drawn on opposite sides of line AB such that AX∣∣BY. If AB and XY intersect each other at P,prove that APX≅BPY (ii) AB and XY bisect each other.
In the given figure, segment AXandBY are equaView SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View Solution