AB is the chord of a circle with centreO. AB is produced to C, such that BC =OB, CO is joined and produced to meet the circle in D.
If ∠ACD=Y∘ and ∠AOD=x∘, Prove that x=3y.
To solve the problem, we will follow a systematic approach to prove that x=3y.
1. Identify the Given Information:
- We have a circle with center O.
- AB is a chord of the circle.
- C is a point such that BC=OB.
- CO is extended to meet the circle at point D.
- Angles given: ∠ACD=y∘ and ∠AOD=x∘.
2. Analyze Triangle OBC:
- Since BC=OB, triangle OBC is isosceles.
- Therefore, the angles opposite to equal sides are equal:
∠OBC=∠OCB=y∘
3. Calculate ∠ABO:
- The angle ∠ABO is the external angle for triangle OBC.
- By the external angle theorem:
∠ABO=∠OBC+∠OCB=y+y=2y
4. Analyze Triangle OAB:
- Since OA=OB (both are radii of the circle), triangle OAB is also isosceles.
- Therefore, ∠OAB=∠OBA=2y.
5. Calculate ∠AOD:
- The angle ∠AOD is the external angle for triangle OAB.
- By the external angle theorem:
∠AOD=∠OAB+∠OBA=2y+2y=4y
6. Relate ∠AOD and ∠ACD:
- We know that ∠AOD can also be expressed in terms of ∠ACD:
∠AOD=∠OAC+∠OCA
- Here, ∠OAC=2y and ∠OCA=y:
∠AOD=2y+y=3y
7. Final Conclusion:
- Therefore, we have:
x=∠AOD=3y
- Hence, we have proved that x=3y.
- We have a circle with center O.
- AB is a chord of the circle.
- C is a point such that BC=OB.
- CO is extended to meet the circle at point D.
- Angles given: ∠ACD=y∘ and ∠AOD=x∘.
- Since BC=OB, triangle OBC is isosceles.
- Therefore, the angles opposite to equal sides are equal:
∠OBC=∠OCB=y∘
- The angle ∠ABO is the external angle for triangle OBC.
- By the external angle theorem:
∠ABO=∠OBC+∠OCB=y+y=2y
- Since OA=OB (both are radii of the circle), triangle OAB is also isosceles.
- Therefore, ∠OAB=∠OBA=2y.
- The angle ∠AOD is the external angle for triangle OAB.
- By the external angle theorem:
∠AOD=∠OAB+∠OBA=2y+2y=4y
- We know that ∠AOD can also be expressed in terms of ∠ACD:
∠AOD=∠OAC+∠OCA
- Here, ∠OAC=2y and ∠OCA=y:
∠AOD=2y+y=3y
- Therefore, we have:
x=∠AOD=3y
- Hence, we have proved that x=3y.
Similar Questions
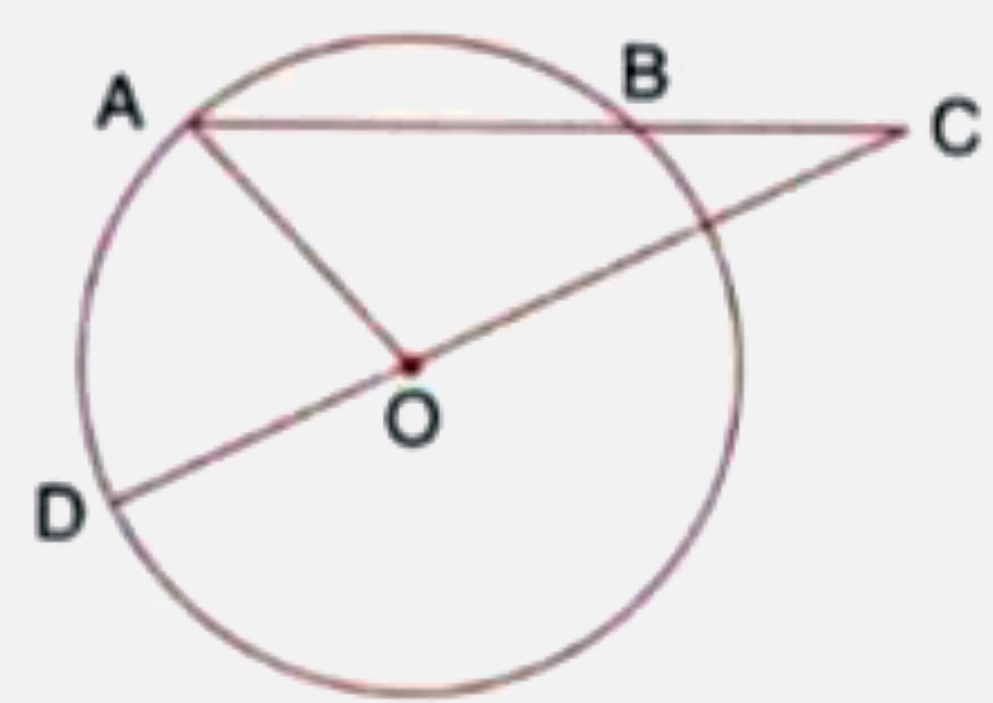
In the figure AB is the chord of a circle with centre O and DOC is a line segment such that BC=DO. If ∠C=20∘, find angle AOD.
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
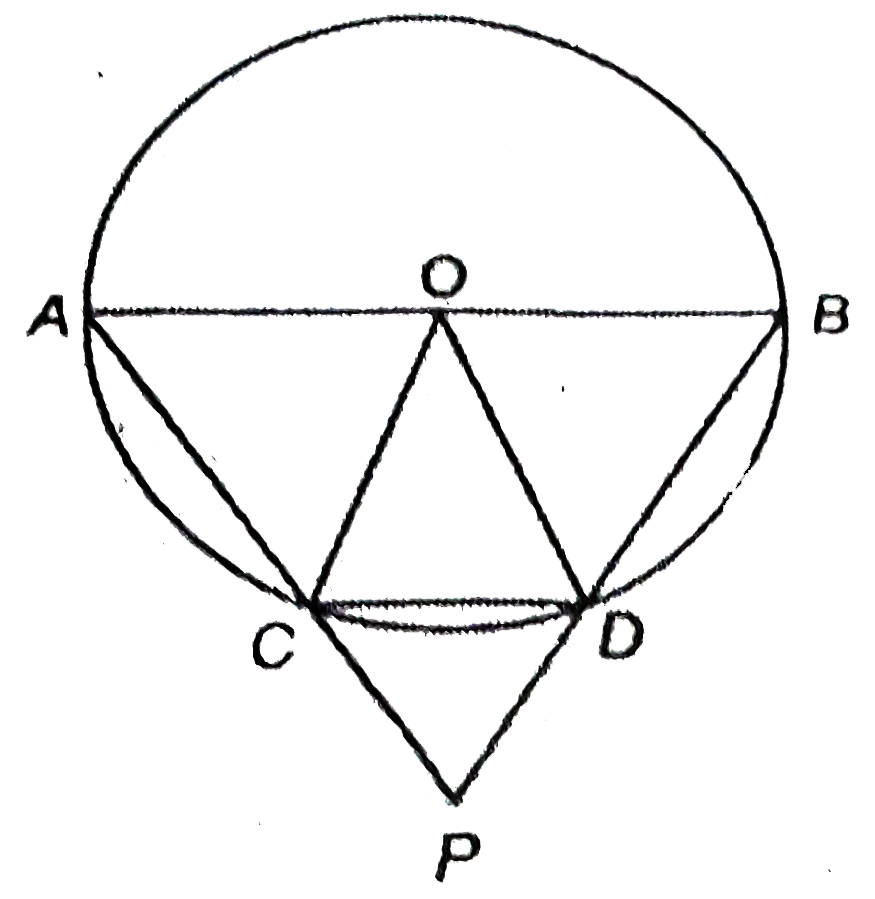
View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
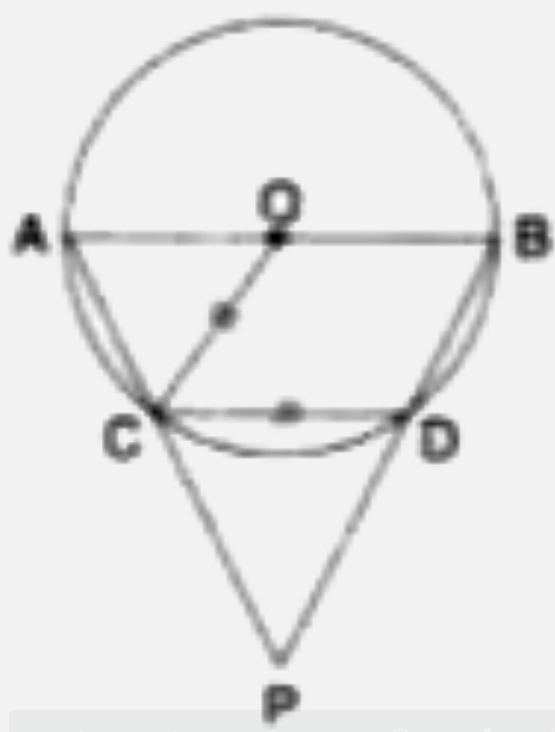
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
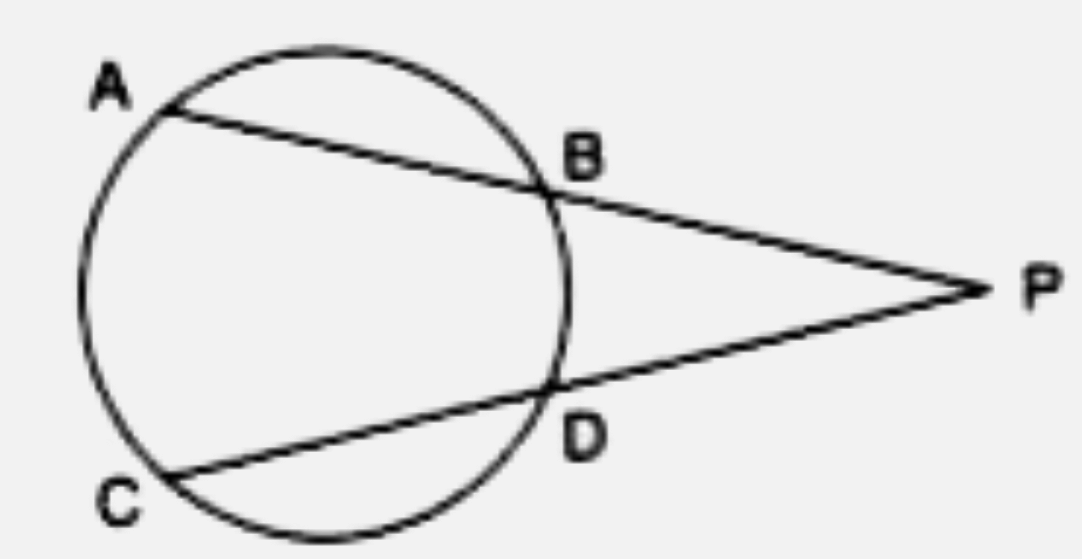
PB=PD
View SolutionDraw a circle of radius 3.5 cm. Mark its centre as O. Take a point A on the circle. Join AO and produce it to meet the circle at B.
Assign a special name to AB.
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :

PA=PC.
View SolutionDraw a circle of radius 3.5 cm. Mark its centre as O. Take a point A on the circle. Join AO and produce it to meet the circle at B.
Measure the length of AB.
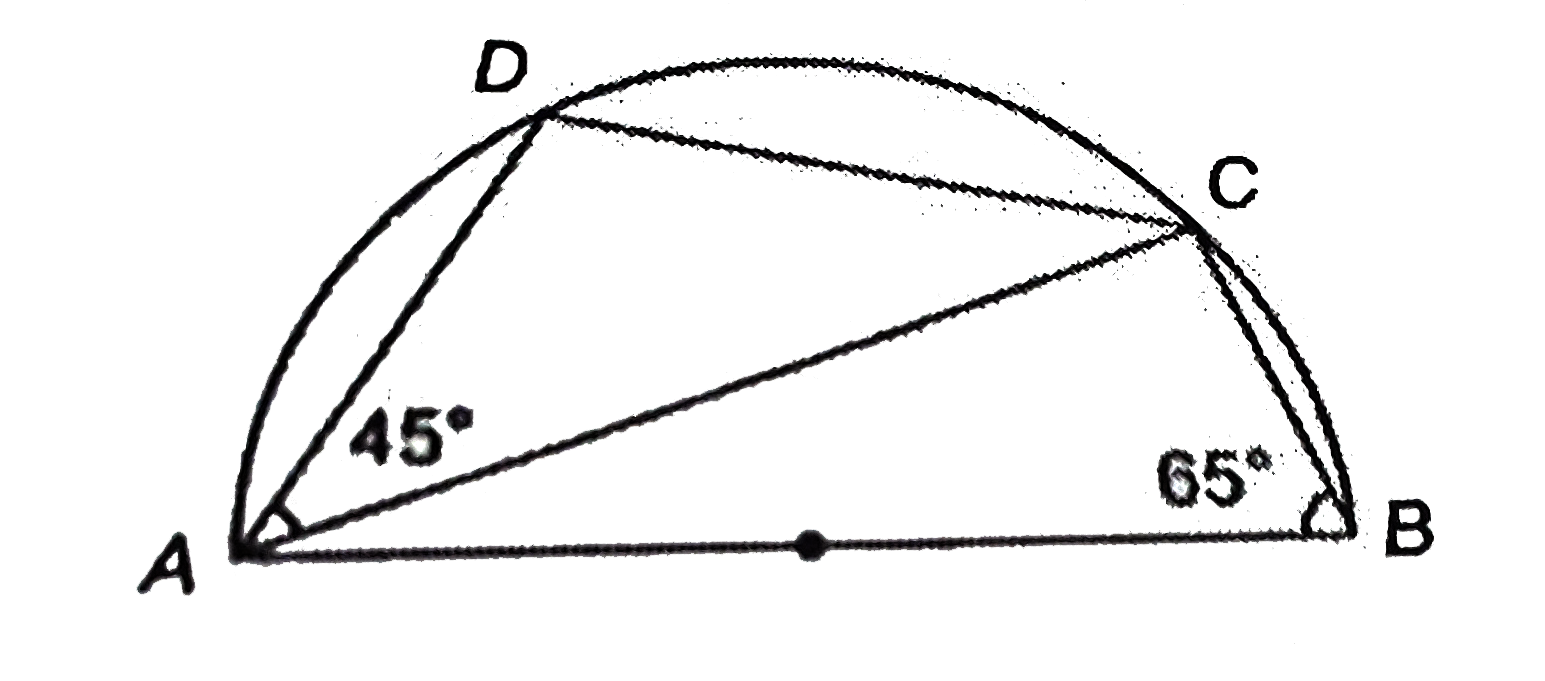
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
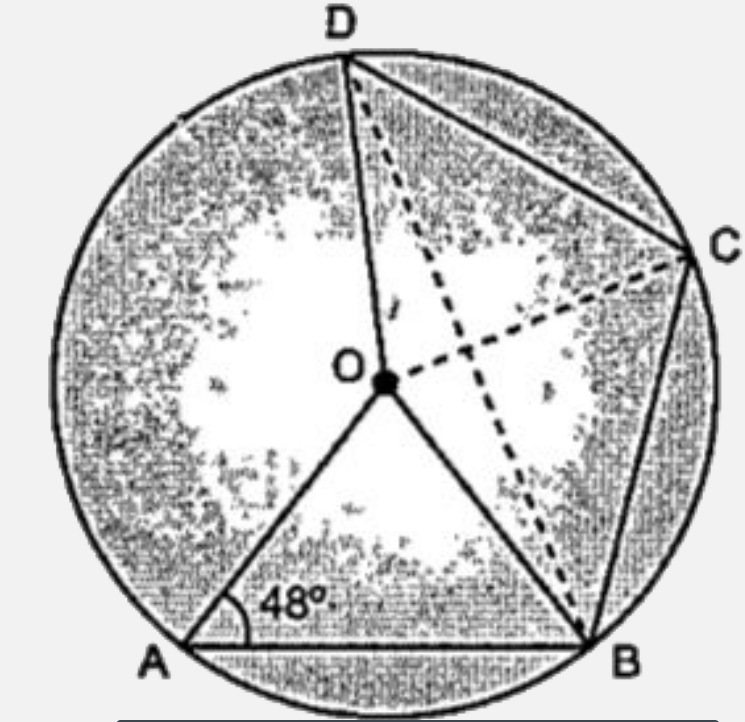
∠OBD
View Solution
